练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）的导函数为f'（x），且f'（x）＜f（x）对任意的x∈R恒成立，则下列不等式均成立的是（ ）
    A.f（ln2）＜2f（0），f（2）＜e2f（0）
    B.f（ln2）＞2f（0），f（2）＞e2f（0）
    C.f（ln2）＜2f（0），f（2）＞e2f（0）
    D.f（ln2）＞2f（0），f（2）＜e2f（0）

    【答案】A
    【解析】解：令g（x）= ，

    则g′（x）= ＜0，

    故g（x）在R递减，

    而ln2＞0，2＞0，

    故g（ln2）＜g（0），g（2）＜g（0），

    即 ＜ ， ＜ ，

    即f（ln2）＜2f（0），f（2）＜e2f（0），

    故选：A．

    【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥S﹣ABCD中，△ABD是正三角形，CB=CD，SC⊥BD．
    （1）求证：SA⊥BD；
    （2）若∠BCD=120°，M为棱SA的中点，求证：DM∥平面SBC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动圆M恒过点（0，1），且与直线y=﹣1相切．
    （1）求圆心M的轨迹方程；
    （2）动直线l过点P（0，﹣2），且与点M的轨迹交于A、B两点，点C与点B关于y轴对称，求证：直线AC恒过定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场销售某种商品的经验表明，该商品每日的销售量y（单位：千克）与销售价格x（单位：元/千克）满足关系式：y= +10（x﹣6）2 ， 其中3＜x＜6，a为常数，已知销售的价格为5元/千克时，每日可以售出该商品11千克．
    （1）求a的值；
    （2）若该商品的成本为3元/千克，试确定销售价格x的值，使商场每日销售该商品所获得的利润最大，并求出最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.

    (1)分别求出两人得分的平均数与方差;

    (2)根据图和上面算得的结果,对两人的训练成绩作出评价.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了研究一种昆虫的产卵数y和温度x是否有关，现收集了7组观测数据列于下表中，并做出了散点图，发现样本点并没有分布在某个带状区域内，两个变量并不呈现线性相关关系，现分别用模型① 与模型；② 作为产卵数y和温度x的回归方程来建立两个变量之间的关系．

    温度x/°C

    20

    22

    24

    26

    28

    30

    32

    产卵数y/个

    6

    10

    21

    24

    64

    113

    322

    t=x2

    400

    484

    576

    676

    784

    900

    1024

    z=lny

    1.79

    2.30

    3.04

    3.18

    4.16

    4.73

    5.77

    26

    692

    80

    3.57

    1157.54

    0.43

    0.32

    0.00012

    其中 ， ，zi=lnyi ， ，
    附：对于一组数据（μ1 ， ν1），（μ2 ， ν2），…（μn ， νn），其回归直线v=βμ+α的斜率和截距的最小二乘估计分别为： ，
    （1）根据表中数据，分别建立两个模型下y关于x的回归方程；并在两个模型下分别估计温度为30°C时的产卵数．（C1 ， C2 ， C3 ， C4与估计值均精确到小数点后两位）（参考数据：e4.65≈104.58，e4.85≈127.74，e5.05≈156.02）
    （2）若模型①、②的相关指数计算分别为 ．，请根据相关指数判断哪个模型的拟合效果更好．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为奇函数， 为偶函数，且．

    （1）求及的解析式及定义域；

    （2）若关于的不等式恒成立，求实数的取值范围．

    （3）如果函数，若函数有两个零点，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的几何体中，四边形是正方形， 平面， 分别为的中点，且.

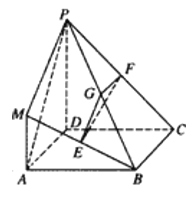
    （1）求证：平面平面；

    （2）求证：平面平面；

    （3）求三棱锥与四棱锥的体积之比.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市出租车的收费标准是：3千米以内(含3千米)，收起步价8元；3千米以上至8千米以内(含8千米)，超出3千米的部分按元/千米收取；8千米以上，超出8千米的部分按2元/千米收取.

    (1)计算某乘客搭乘出租车行驶7千米时应付的车费；

    (2)试写出车费 (元)与里程 (千米)之间的函数解析式并画出图像；

    (3)小陈周末外出，行程为10千米，他设计了两种方案：

    方案1：分两段乘车，先乘一辆行驶5千米，下车换乘另一辆车再行5千米至目的地

    方案2：只乘一辆车至目的地，试问：以上哪种方案更省钱，请说明理由.

    查看答案和解析>>

    同步练习册答案