选修4-5:不等式选讲
设f(x)=|x-a|,a∈R.
(I)当-1≤x≤3时,f(x)≤3,求a的取值范围;
(II)若对任意x∈R,f(x-a)+f(x+a)≥1-2a恒成立,求实数a的最小值.
解:(Ⅰ)f(x)=|x-a|≤3,即a-3≤x≤a+3.
依题意,
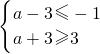
由此得a的取值范围是[0,2].…(4分)
(Ⅱ)f(x-a)+f(x+a)=|x-2a|+|x|≥|(x-2a)-x|=2|a|.…(6分)
当且仅当(x-2a)x≤0时取等号.
解不等式2|a|≥1-2a,得a≥

.
故a的最小值为

.…(10分)
分析:(I)当-1≤x≤3时,f(x)=|x-a|≤3,即a-3≤x≤a+3.由此建立关于a的不等关系能求出a的取值范围.
(II)根据绝对值不等式的性质得|x-2a|+|x|最小值就是2|a|,若f(x-a)+f(x+a)≥1-2a对x∈R恒成立,则只要满足2|a|≥1-2a,由此能求出实数a的最小值.
点评:本题考查不等式的解集的求法,考查满足条件的实数的最小值的求法,解题时要认真审题,注意零点分段讨论法和绝对值不等式性质的合理运用.

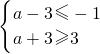
 .
. .…(10分)
.…(10分)

 阅读快车系列答案
阅读快车系列答案