考点:数列的求和,数列递推式
专题:综合题,等差数列与等比数列
分析:(1)先求出S
n,然后利用当n≥2时,a
n=S
n-S
n-1代入求解,最后验证首项即可;
(2)由a
n=2n-14≤0,可得n≤7,即可指出n取何值时S
n取得最小值,并求出S
n的最小值;
(3)求出数列{b
n}的通项,可得数列{b
n}是以
为首项,
为公比的等比数列,利用等比数列的求和公式,即可求数列{b
n}的前n项和为T
n.
解答:
解:(1)∵点(n,
),n∈N
*在直线y=x-13,
∴
=n-13,S
n=n
2-13n.
当n≥2时,a
n=S
n-S
n-1=(n
2-13n)-[(n-1)
2-12(n-1)]=2n-14;
当n=1时,a
1=S
1=-12,符合题意.
所以a
n=2n-14(n∈N
*).
(2)a
n=2n-14≤0,∴n≤7,
∴n取6或7时S
n取得最小值,S
n的最小值为
=-42;
(3)b
n=(
)
an+13=
()2n-1,
∴
=
,b
1=
,
∴数列{b
n}是以
为首项,
为公比的等比数列,
∴数列{b
n}的前n项和为T
n=
=
(1-
).
点评:本题重点考查等差数列、等比数列的通项公式以及数列的求和公式,同时考查了学生的计算能力、分析解决问题的能力,属于中档题.



 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案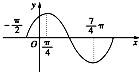 函数f(x)=Asin(ωx+φ)的图象如图所示.试依图推出:
函数f(x)=Asin(ωx+φ)的图象如图所示.试依图推出: