【题目】已知x＝﹣1是函数f（x）
x3
（a2+a﹣3）x2+（2a+2）x的极大值点，则实数a＝（ ）
A.0B.0或﹣3C.0或3D.﹣3
【答案】D
【解析】
由f（x）
x3
（a2+a﹣3）x2+（2a+2）x，求导得
=x2
（a2+a﹣3）x+（2a+2），根据x＝﹣1是函数f（x）x3（a2+a﹣3）x2+（2a+2）x的极大值点，有
=1+（a2+a﹣3）+（2a+2）=0，解得a=0或 a=-3.然后分别验证x＝﹣1是否是极值点且为极大值点即可.
因为f（x）x3（a2+a﹣3）x2+（2a+2）x，
所以=x2（a2+a﹣3）x+（2a+2），
已知x＝﹣1是函数f（x）x3（a2+a﹣3）x2+（2a+2）x的极大值点，
所以=1+（a2+a﹣3）+（2a+2）=0，
解得a=0或
当a=0时，
，
当
，当
所以x＝﹣1是函数f（x）x3（a2+a﹣3）x2+（2a+2）x的极小值点，不符合题意.
当 时，
，
当
，当
所以x＝﹣1是函数f（x）x3（a2+a﹣3）x2+（2a+2）x的极大值点，符合题意.
故选：D
科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝|2x+3|+|2x﹣1|．
（1）求不等式f（x）≤6的解集；
（2）若关于x的不等式f（x）＜|m﹣1|的解集非空，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
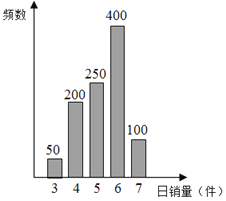
【题目】某公司销售部随机抽取了1000名销售员1天的销售记录，经统计，其柱状图如图．
该公司给出了两种日薪方案．
方案1：没有底薪，每销售一件薪资20元；
方案2：底薪90元，每日前5件的销售量没有奖励，超过5件的部分每件奖励20元．
（1）分别求出两种日薪方案中日工资y（单位：元）与销售件数n的函数关系式；
（2）若将频率视为概率，回答下列问题：
（Ⅰ）根据柱状图，试分别估计两种方案的日薪X（单位：元）的数学期望及方差；
（Ⅱ）如果你要应聘该公司的销售员，结合（Ⅰ）中的数据，根据统计学的思想，分析选择哪种薪资方案比较合适，并说明你的理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝x＋2x，g(x)＝x＋ln x，h(x)＝x－
－1的零点分别为x1，x2，x3，则x1，x2，x3的大小关系是________(由小到大).
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知幂函数f（x）＝（3m2﹣2m）x
在（0，+∞）上单调递增，g（x）＝x2﹣4x+t．
（1）求实数m的值；
（2）当x∈[1，9]时，记f（x），g（x）的值域分别为集合A，B，设命题p：x∈A，命题q：x∈B，若命题p是命题q的充分不必要条件，求实数t的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PPD//平面MAC，PA=PD=
，AB=4．
（I）求证：M为PB的中点；
（II）求二面角B-PD-A的大小；
（III）求直线MC与平面BDP所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解高三学生的“理科综合”成绩是否与性别有关，某校课外学习兴趣小组在本地区高三年级理科班中随机抽取男、女学生各100名，然后对这200名学生在一次联合模拟考试中的“理科综合”成绩进行统计规定：分数不小于240分为“优秀”小于240分为“非优秀”．
（1）根据题意，填写下面的2×2列联表，并根据列联表判断是否有90%以上的把握认为“理科综合”成绩是否优秀与性别有关．
性别 | 优秀 | 非优秀 | 总计 |
男生 | 35 | ||
女生 | 75 | ||
总计 |
（2）用分层抽样的方法从成绩优秀的学生中随机抽取12名学生，然后再从这12名学生中抽取3名参加某高校举办的自主招生考试，设抽到的3名学生中女生的人数为X，求X的分布列及数学期望．
附：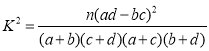
，其中
．
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
