
���� ����֪�еĹ�ϵʽ����������ʽ����ʽ�ӵı仯���ɣ������ܽ�ɵô𰸣�
��� �⣺����֪�й�ϵʽ��
��$\frac{1}{2}$+$\frac{1}{3}$��ln3��
��$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$��ln5��
��$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$+$\frac{1}{7}$��ln7��
��
���ɿɵã�
����ʽʽ�������2n����ʽ�ĺͣ����Ӿ�Ϊ1����ĸ��2��2n+1��
����ʽ�ұ���һ����Ȼ����ʽ������Ϊ2n+1��
��һ�����Ϊ��$\frac{1}{2}$+$\frac{1}{3}$+��+$\frac{1}{2n+1}$��ln��2n+1����
�ʴ�Ϊ��$\frac{1}{2}$+$\frac{1}{3}$+��+$\frac{1}{2n+1}$��ln��2n+1��
���� ����������һ�㲽���ǣ���1��ͨ���۲�����������ijЩ��ͬ���ʣ���2������֪����ͬ�������Ƴ�һ����ȷ�����һ�������⣨���룩��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | -$\frac{��}{6}$ | C�� | $\frac{3}{2}��$ | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5��10��15��20��25 | B�� | 5��12��31��39��57 | C�� | 5��17��29��41��53 | D�� | 5��15��25��35��45 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
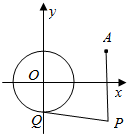 ��ͼ����֪ԲO��x2+y2=1�Ͷ���A��2��1������ԲO��һ��P��ԲO������PQ���е�ΪQ������|PQ|=|PA|��
��ͼ����֪ԲO��x2+y2=1�Ͷ���A��2��1������ԲO��һ��P��ԲO������PQ���е�ΪQ������|PQ|=|PA|���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{10\sqrt{6}}{3}$ | B�� | $\frac{14\sqrt{6}}{3}$ | C�� | 4$\sqrt{3}$ | D�� | 6$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com