
【题目】在正四面体P﹣ABC体积为V,现内部取一点S,则 ![]() 的概率为( )
的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
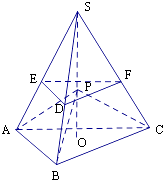
【解析】解:作出P在底面△ABC的射影为O,
若VS﹣ABC= ![]() VS﹣ABC,则高OS=
VS﹣ABC,则高OS= ![]() OP,
OP,
分别取PA、PB、PC上的点E、F、D,
并使SE=2EA,SF=2FC,SD=2DB,如图
并连结EF、FD、DE,则平面EFD∥平面ABC.
当点S在正四面体P﹣EFD内部运动时,
即此时S在三棱锥VP﹣ABC的中垂面DEF上,
满足VS﹣ABC< ![]() VP﹣ABC的点P位于在三棱锥VP﹣ABC的中垂面DEF以下的棱台内,
VP﹣ABC的点P位于在三棱锥VP﹣ABC的中垂面DEF以下的棱台内,
同理,VS﹣ABC> ![]() VP﹣ABC的S在距离ABC为
VP﹣ABC的S在距离ABC为 ![]() OS的平面以上的棱锥内,
OS的平面以上的棱锥内,
所以满足 ![]() 的棱台体积为(1
的棱台体积为(1 ![]() )﹣(1﹣
)﹣(1﹣ ![]() )=
)= ![]() ;
;
由几何概型,满足“ ![]() ”的概率为
”的概率为 ![]() ,
,
故选A.
【考点精析】本题主要考查了几何概型的相关知识点,需要掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等才能正确解答此题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各两张,让孩子从盒子里任取3张卡片,按卡片上的最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字
(1)求取出的3张卡片上的数字互不相同的概率;
(2)求随机变量X的分布列及数学期望;
(3)若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过左焦点F且垂直于x轴的弦长为1.
,过左焦点F且垂直于x轴的弦长为1.
(I)求椭圆C的标准方程;
(Ⅱ)点P(m,0)为椭圆C的长轴上的一个动点,过点P且斜率为 ![]() 的直线l交椭圆C于A,B两点,问:|PA|2+|PB|2是否为定值?若是,求出这个定值并证明,否则,请说明理由.
的直线l交椭圆C于A,B两点,问:|PA|2+|PB|2是否为定值?若是,求出这个定值并证明,否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,
, ![]() ,使得
,使得![]() 的解集恰好是
的解集恰好是![]() ,若存在,求出
,若存在,求出![]() ,
, ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线C的参数方程: ![]() ,直线l的参数方程为
,直线l的参数方程为 ![]() .
.
(1)若直线l与曲线C只有一个公共点,求实数a;
(2)若点P,Q分别为直线l与曲线C上的动点,若 ![]() ,求实数a.
,求实数a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
|
|
|
|
| 0 | 5 | 0 | -5 | 0 |
(1)求出实数![]() ;
;
(2)求出函数![]() 的解析式;
的解析式;
(3)将![]() 图像上所有点向左平移
图像上所有点向左平移![]() 个单位长度,得到
个单位长度,得到![]() 图像,求
图像,求![]() 的图像离原点
的图像离原点![]() 最近的对称中心.
最近的对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是四棱锥的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点,在此几何体中,给出下面四个结论中错误的是( )

A. 平面![]() 平面ABCD
平面ABCD
B. 直线BE,CF相交于一点
C. EF//平面BGD
D. ![]() 平面BGD
平面BGD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com