

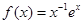 的定义域为
的定义域为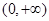 .
.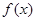 在
在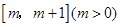 上的最小值;
上的最小值;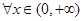 ,不等式
,不等式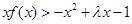 恒成立,求
恒成立,求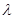 的取值范围.
的取值范围.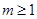 时,
时,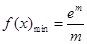 ,当
,当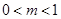 时,
时,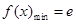 ;(2)
;(2)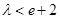 .
.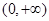 上的单调区间,然后考察区间
上的单调区间,然后考察区间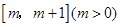 与其关系,根据需要对
与其关系,根据需要对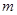 分类讨论;(Ⅱ)不等式恒成立问题,通常可以通过分离参数转化为求函数的最值问题,如本题分离参数后可得到,
分类讨论;(Ⅱ)不等式恒成立问题,通常可以通过分离参数转化为求函数的最值问题,如本题分离参数后可得到, ,然后转化为求左边函数的最小值问题,可用导数判断其单调性,再求出最小值,
,然后转化为求左边函数的最小值问题,可用导数判断其单调性,再求出最小值,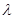 小于这个最小值即可.对于不等式恒成立问题通常可以通过分离参数或直接考察函数的性质解决,一般来说方便分离参数的还是分离参数,这样在研究函数的性质时可避开参变数的影响,便于解决问题.
小于这个最小值即可.对于不等式恒成立问题通常可以通过分离参数或直接考察函数的性质解决,一般来说方便分离参数的还是分离参数,这样在研究函数的性质时可避开参变数的影响,便于解决问题.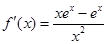 , 1分
, 1分 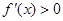 得
得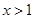 ;令
;令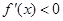 得
得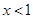
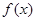 在
在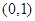 上是减函数;在
上是减函数;在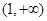 上是增函数 3分
上是增函数 3分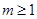 时,函数
时,函数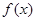 在
在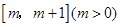 上是增函数,
上是增函数,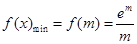 5分
5分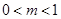 时,函数
时,函数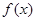 在
在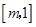 上是减函数;在
上是减函数;在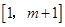 上是增函数
上是增函数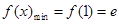 7分
7分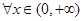 ,不等式
,不等式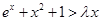 恒成立
恒成立 恒成立 9分
恒成立 9分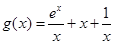 ,则
,则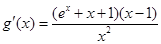 11分
11分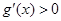 得
得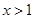 ;由
;由 得
得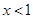 13分
13分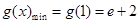 。 所以,
。 所以,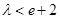 . 14分
. 14分

 目标测试系列答案
目标测试系列答案科目:高中数学 来源:不详 题型:解答题
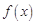 的导函数
的导函数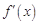 是二次函数,当
是二次函数,当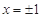 时,
时,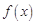 有极值,且极大值为2,
有极值,且极大值为2,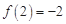 .
.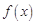 的解析式;
的解析式;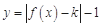 有两个零点,求实数
有两个零点,求实数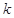 的取值范围;
的取值范围;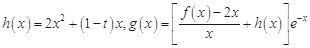 ,若存在实数
,若存在实数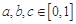 ,使得
,使得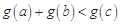 ,求
,求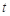 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
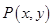 为函数
为函数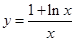 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线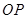 的斜率
的斜率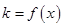 .
.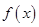 在区间
在区间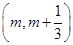
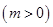 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;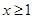 时,不等式
时,不等式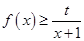 恒成立,求实数
恒成立,求实数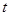 的取值范围;
的取值范围;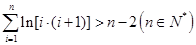 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com