
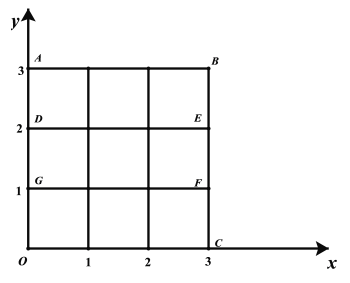
【题目】平面直角坐标系中有16个格点(i,j),其中0≤i≤3,0≤j≤3.若在这16个点中任取n个点,这n个点中总存在4个点,这4个点是一个正方形的顶点,求n的最小值.
【答案】11.
【解析】
分两步来证明:先找到10个点,它们中的任意四点不能构成正方形的顶点,再根据抽屉原理证明任意的11个点,一定存在4个点为正方形的四个顶点.
存在下面的10点即:
点(0,0),(1,0),(2,0),(2,1),(3,1),(0,2),(3,2),(0,3),(1,3),(3,3),
其中任意4个点不能构成正方形的顶点,故![]() .
.
下证:任意11点中,一定存在4个点为正方形的四个顶点.
因为共取11个点,分两种情况讨论:
(1)有一行有4个点(设为![]() ),则余下三行共有7个点,
),则余下三行共有7个点,
由抽屉原理知余下三行中必有一行至少有3个点(设为![]() ),
),
因![]() ,
,![]() 分布在两行,
分布在两行,
若该两行相邻或中间隔一行,则存在四个点,它们为正方形的四个顶点;
若该两行间隔两行,如图,不妨设![]() 为线段
为线段![]() 上的格点,
上的格点,![]() 为线段
为线段![]() 上的格点,对应的点的坐标为
上的格点,对应的点的坐标为![]() ,
,
余下4个点分布在中间两行,若线段![]() 上有两个整点,则它们和
上有两个整点,则它们和![]() 中的两点构成正方形的顶点,否则线段
中的两点构成正方形的顶点,否则线段![]() 上至少有3个点,则其中必有两个格点与
上至少有3个点,则其中必有两个格点与![]() 中的两点构成正方形的顶点.
中的两点构成正方形的顶点.
(2)任意一行都没有4个点,则各行的格点数分别为![]() ,故4行中必有相邻两行各有3个格点,这6个格点中必存在4个格点,它们构成正方形的顶点.
,故4行中必有相邻两行各有3个格点,这6个格点中必存在4个格点,它们构成正方形的顶点.


科目:高中数学 来源: 题型:
【题目】随着疫情的有效控制,人们的生产生活逐渐向正常秩序恢复,位于我区的某著名赏花园区重新开放.据统计硏究,近期每天赏花的人数大致符合以下数学模型![]() .以
.以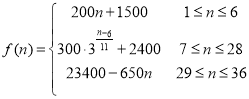 表示第
表示第![]() 个时刻进入园区的人数,以
个时刻进入园区的人数,以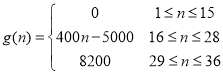 表示第
表示第![]() 个时刻离开园区的人数,设定每15分钟为一个计算单位,上午8点15分作为第1个计算人数单位,即
个时刻离开园区的人数,设定每15分钟为一个计算单位,上午8点15分作为第1个计算人数单位,即![]() 点30分作为第2个计算单位,即
点30分作为第2个计算单位,即![]() :依次类推,把一天内从上午8点到下午5点分成36个计算单位(最后结果四舍五入,精确到整数)
:依次类推,把一天内从上午8点到下午5点分成36个计算单位(最后结果四舍五入,精确到整数)
(1)试分别计算当天12:30至13:30这一小时内,进入园区的人数![]() 和离开园区的游客人数
和离开园区的游客人数![]() .
.
(2)请问,从12点(即![]() )开始,园区内总人数何时达到最多?并说明理由
)开始,园区内总人数何时达到最多?并说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,一场新冠肺炎疫情突如其来,在党中央强有力的领导下,全国各地的医务工作者迅速驰援湖北,以大无畏的精神冲在了抗击疫情的第一线,迅速控制住疫情.但国外疫情严峻,输入性病例逐渐增多,为了巩固我国的抗疫成果,保护国家和人民群众的生命安全,我国三家生物高科技公司各自组成A、B、C三个科研团队进行加急疫苗研究,其研究方向分别是灭活疫苗、核酸疫苗和全病毒疫苗,根据这三家的科技实力和组成的团队成员,专家预测这A、B、C三个团队未来六个月中研究出合格疫苗并用于临床接种的概率分别为![]() ,
,![]() ,
,![]() ,且三个团队是否研究出合格疫苗相互独立.
,且三个团队是否研究出合格疫苗相互独立.
(1)求六个月后A,B两个团队恰有一个研究出合格疫苗并用于临床接种的概率;
(2)设六个月后研究出合格疫苗并用于临床接种的团队个数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:![]() 和椭圆
和椭圆![]() :
:![]() 相交于点
相交于点![]() ,
,![]()
(1)当直线l过椭圆![]() 的左焦点和上顶点时,求直线l的方程
的左焦点和上顶点时,求直线l的方程
(2)点![]() 在
在![]() 上,若
上,若![]() ,求
,求![]() 面积的最大值:
面积的最大值:
(3)如果原点O到直线l的距离是![]() ,证明:
,证明:![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地有一块半径为R的扇形AOB公园,其中O为扇形所在圆的圆心,AOB=![]() ,OA,OB,
,OA,OB,![]() 为公园原有道路.为满足市民观赏和健身的需要,市政部门拟在
为公园原有道路.为满足市民观赏和健身的需要,市政部门拟在![]() 上选取一点M,新建道路OM及与OA平行的道路MN(点N在线段OB上),设AOM=
上选取一点M,新建道路OM及与OA平行的道路MN(点N在线段OB上),设AOM=![]() .
.

(1)如何设计,才能使市民从点O出发沿道路OM,MN行走至点N所经过的路径最长?请说明理由;
(2)如何设计,才能使市民从点A出发沿道路![]() ,MN行走至点N所经过的路径最长?请说明理由.
,MN行走至点N所经过的路径最长?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
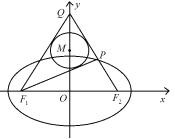
【题目】如图,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() ,
,![]() 是
是![]() 轴的正半轴上一点,
轴的正半轴上一点,![]() 交椭圆于
交椭圆于![]() ,且
,且![]() ,
,![]() 的内切圆
的内切圆![]() 半径为1.
半径为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 和圆
和圆![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某原料在市场上从2013年至2019年这7年中每年的平均价格(单位:千元/吨)数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
平均价格 (单位:千元/吨) |
|
|
|
|
|
|
|
(![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程(系数精确到
为预报变量的线性回归方程(系数精确到![]() );
);
(2)以(1)的结论为依据,预测2032年该原料价格.预估该原料价格在哪一年突破1万元/吨?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: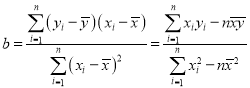 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足
满足![]() ,且存在常数
,且存在常数![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() ,则称数列
,则称数列![]() 为“k控数列”.
为“k控数列”.
(1)若公差为d的等差数列![]() 是“2控数列”,求d的取值范围;
是“2控数列”,求d的取值范围;
(2)已知公比为![]() 的等比数列
的等比数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 与
与![]() 都是“k控数列”,求q的取值范围(用k表示).
都是“k控数列”,求q的取值范围(用k表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com