
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 为
为![]() 的菱形,
的菱形, ![]() .
.
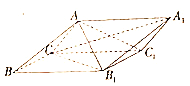
(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】【试题分析】(1) 连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,根据菱形的几何性质与等腰三角形的几何性质可知
,根据菱形的几何性质与等腰三角形的几何性质可知![]() ,
, ![]() ,由此证得
,由此证得![]()
![]() 平面
平面![]() ,故平面
,故平面![]()
![]() 平面
平面![]() .(2) 以
.(2) 以![]() 为坐标原点,
为坐标原点, ![]() 的方向为
的方向为![]() 轴正方向建立空间直角坐标系,通过计算直线
轴正方向建立空间直角坐标系,通过计算直线![]() 的方向向量与平面
的方向向量与平面![]() 的法向量,来求得直线与平面所成角的正弦值.
的法向量,来求得直线与平面所成角的正弦值.
【试题解析】
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]()
![]() 侧面
侧面![]() 为菱形,
为菱形, ![]()
![]()
![]()
![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]()
![]()
又![]() ,
, ![]()
![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 平面
平面![]() .
.
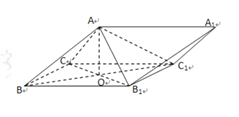
(2)由![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
![]()
![]()
从而![]() ,
, ![]() ,
, ![]() 两两互相垂直,以
两两互相垂直,以![]() 为坐标原点,
为坐标原点, ![]() 的方向为
的方向为![]() 轴正方向,建立如图所示空间直角坐标系
轴正方向,建立如图所示空间直角坐标系![]()
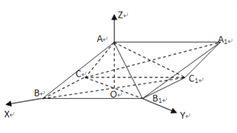
![]() 直线
直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
, ![]()
![]()
设![]() ,则
,则![]() ,又
,又![]() ,
, ![]() △
△![]() 是边长为2的等边三角形
是边长为2的等边三角形
![]()
![]() ,
,
![]()
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则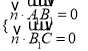 即
即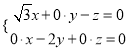
令![]() 则
则![]()
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
则
![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,已知过点
,已知过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为: (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)写出曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(2)若![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A. 若![]() ,则“
,则“![]() ”的充分条件是“
”的充分条件是“![]() ”
”
B. 若![]() ,则“
,则“![]() ”的充要条件是“
”的充要条件是“![]() ”
”
C. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
D. ![]() 是等比数列,则
是等比数列,则![]() 是
是![]() 为单调递减数列的充分条件
为单调递减数列的充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加.下表是某购物网站2017年1-8月促销费用(万元)和产品销量(万件)的具体数据.

(1)根据数据可知![]() 与
与![]() 具有线性相关关系,请建立
具有线性相关关系,请建立![]() 关于
关于![]() 的回归方程
的回归方程![]() (系数精确到
(系数精确到![]() );
);
(2)已知6月份该购物网站为庆祝成立1周年,特制定奖励制度:以![]() (单位:件)表示日销量,
(单位:件)表示日销量, ![]() ,则每位员工每日奖励100元;
,则每位员工每日奖励100元; ![]() ,则每位员工每日奖励150元;
,则每位员工每日奖励150元; ![]() ,则每位员工每日奖励200元.现已知该网站6月份日销量
,则每位员工每日奖励200元.现已知该网站6月份日销量![]() 服从正态分布
服从正态分布![]() ,请你计算某位员工当月奖励金额总数大约多少元.(当月奖励金额总数精确到百分位)
,请你计算某位员工当月奖励金额总数大约多少元.(当月奖励金额总数精确到百分位)
参考数据: ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量, ![]() .
.
参考公式:
(1)对于一组数据![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为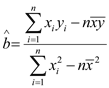 ,
, ![]() .
.
(2)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=excos x-x.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在图所示的五面体中,面ABCD为直角梯形,![]() ,平面
,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() 是边长为2的正三角形.
是边长为2的正三角形.

![]() 证明:
证明:![]() 平面ACF;
平面ACF;
![]() 若点P在线段EF上,且二面角
若点P在线段EF上,且二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为直角梯形,且
为直角梯形,且![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() .
.

(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )若二面角
)若二面角![]() 为直二面角,
为直二面角,
(i)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
(ii)棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求定义域,并判断函数f(x)的奇偶性;
(2)若f(1)+f(2)=0,证明函数f(x)在(0,+∞)上的单调性,并求函数f(x)在区间[1,4]上的最值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com