
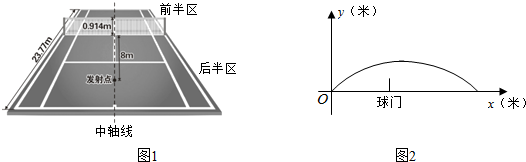
分析 (Ⅰ)由$\frac{1}{2}kx-\frac{1}{80}(1+{k^2}){x^2}=0$得:x=$\frac{40k}{1+{k}^{2}}$或x=0,利用基本不等式求发射器的最大射程;
(Ⅱ)求出$\frac{1}{2}$<k<$\frac{9}{2}$,依题意:关于k的方程$\frac{1}{2}$ka-$\frac{1}{80}$(1+k2)a2=255在($\frac{1}{2}$,$\frac{9}{2}$)上有实数解,即可得出结论.
解答 解:(Ⅰ)由$\frac{1}{2}kx-\frac{1}{80}(1+{k^2}){x^2}=0$得:x=$\frac{40k}{1+{k}^{2}}$或x=0,
由x=$\frac{40}{k+\frac{1}{k}}$≤$\frac{40}{2}$=20,当且仅当k=1时取等号.
因此,最大射程为20米;
(Ⅱ)网球发过球网,满足x=8时y>1.
所以4k-$\frac{4}{5}$(1+k2)>1,即4k2-20k+9<0,
因此$\frac{1}{2}$<k<$\frac{9}{2}$
依题意:关于k的方程 $\frac{1}{2}$ka-$\frac{1}{80}$(1+k2)a2=255在($\frac{1}{2}$,$\frac{9}{2}$)上有实数解
即 a2k2-40ak+a2+204(a≠0)
△=1600a2-4a2(a2+204)≥0
得a≤14,
此时k=$\frac{10}{7}$,球过网了,
所以击球点的横坐标 a最大为14
点评 本题考查利用数学知识解决实际问题,考查基本不等式的运用,考查学生的计算能力,正确转化是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com