
 在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4,∠PAB=60°
在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4,∠PAB=60° 分析 (I)取PC的中点G,连结DG,EG,根据已知条件容易说明四边形ADGE为平行四边形,从而有AE∥DG,根据线面平行的判定定理即得到AE∥平面PCD;
(Ⅱ)三棱锥P-BDG的体积=$\frac{1}{2}$VP-BDC,即可求三棱锥P-BDG的体积.
解答  (I)证明:如图,取PC的中点G,连结DG,EG;
(I)证明:如图,取PC的中点G,连结DG,EG;
∵EG∥AD,且AD=EG,所以ADGE为平行四边形;
∴AE∥DG,且AE?平面PCD,DG?平面PCD;
∴AE∥平面PCD;
(II)解:侧面PAB⊥底面ABCD,PA=AB=2,∠PAB=60°,
∴P到平面BDC的距离为$\sqrt{3}$,
底面ABCD为直角梯形,AD∥BC,AB⊥BC,AD=AB=2,BC=4,∴S△BDC=$\frac{1}{2}×4×2$=4
三棱锥P-BDG的体积=$\frac{1}{2}$VP-BDC=$\frac{1}{2}×4×\sqrt{3}$=2$\sqrt{3}$.
点评 考查中位线的性质,平行四边形的定义,线面平行的判定定理,以及直角三角形边的关系,面面垂直的性质定理,棱锥的体积公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
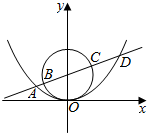 如图所示,过抛物线x2=4py(p>0)焦点的直线依次交抛物线与圆x2+(y-p)2=p2于点A,B,C,D,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值是( )
如图所示,过抛物线x2=4py(p>0)焦点的直线依次交抛物线与圆x2+(y-p)2=p2于点A,B,C,D,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值是( )| A. | 8p2 | B. | 4p2 | C. | 2p2 | D. | p2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com