
【题目】已知定义:在数列{an}中,若a ![]() ﹣a
﹣a ![]() =p(n≥2,n∈N* , p为常数),则称数列{an}为等方差数列,下列判断:
=p(n≥2,n∈N* , p为常数),则称数列{an}为等方差数列,下列判断:
①若{an}是“等方差数列”,则数列{an2}是等差数列;
②{(﹣1)n}是“等方差数列”;
③若{an}是“等方差数列”,则数列{akn}(k∈N* , k为常数)不可能还是“等方差数列”;
④若{an}既是“等方差数列”,又是等差数列,则该数列是常数列.
其中正确的结论是 . (写出所有正确结论的编号)
【答案】①②④
【解析】解:①{an}是“等方差数列”,∴a ![]() ﹣a
﹣a ![]() =p(n≥2,n∈N* , p为常数),则数列{an2}是等差数列,正确;
=p(n≥2,n∈N* , p为常数),则数列{an2}是等差数列,正确;
②∵an=(﹣1)n , ∴ ![]() =1,则n≥2时,a
=1,则n≥2时,a ![]() ﹣a
﹣a ![]() ,=0,∴数列{an}为等方差数列,正确;
,=0,∴数列{an}为等方差数列,正确;
③{an}是“等方差数列”,则数列{akn}(k∈N* , k为常数)可能还是“等方差数列”,取an=2满足条件,因此不正确;
④若{an}既是“等方差数列”,又是等差数列,设公差为d,∴n≥2时,a ![]() ﹣a
﹣a ![]() =
= ![]()
![]() =d[2a1+(2n﹣3)d]为常数,必然d=0,
=d[2a1+(2n﹣3)d]为常数,必然d=0,
则该数列是常数列,正确.
所以答案是:①②④.
【考点精析】根据题目的已知条件,利用等差数列的性质的相关知识可以得到问题的答案,需要掌握在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在![]() 内的产品为合格品,否则为不合格品,统计结果如表:
内的产品为合格品,否则为不合格品,统计结果如表:
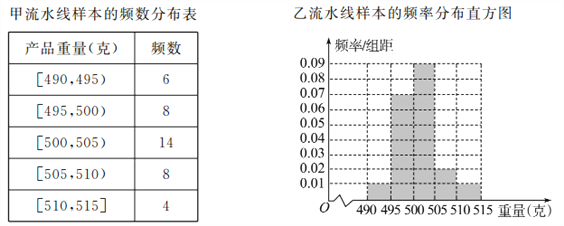
(Ⅰ)求甲流水线样本合格的频率;
(Ⅱ)从乙流水线上重量值落在![]() 内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中,选出适当的一种填空:
(1)记集合A={-1,p,2},B={2,3},则“p=3”是“A∩B=B”的__________________;
(2)“a=1”是“函数f(x)=|2x-a|在区间![]() 上为增函数”的________________.
上为增函数”的________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明计划在8月11日至8月20日期间游览某主题公园.根据旅游局统计数据,该主题公园在此期间“游览舒适度”(即在园人数与景区主管部门核定的最大瞬时容量之比,40%以下为舒适,40%—60%为一般,60%以上为拥挤)情况如图所示.小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览2天.
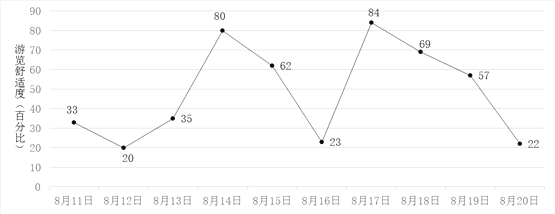 (Ⅰ)求小明连续两天都遇上拥挤的概率;
(Ⅰ)求小明连续两天都遇上拥挤的概率;
(Ⅱ)设![]() 是小明游览期间遇上舒适的天数,求
是小明游览期间遇上舒适的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)由图判断从哪天开始连续三天游览舒适度的方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
(2)过点P(0,3)的直线m与轨迹C交于A,B两点,若A是PB的中点,求直线m的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为菱形,且
为菱形,且![]() ,
, ![]() ,
, ![]() ∥
∥![]() ,
, ![]() 为
为![]() 中点.
中点.
(Ⅰ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使
,使![]()
![]() ? 若存在,求
? 若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=2,an+1=4an﹣3n+1,n∈N* .
(1)证明数列{an﹣n}是等比数列;
(2)求数列{an}的前n项和Sn;
(3)证明不等式Sn+1≤4Sn , 对任意n∈N*皆成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非零向量 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 满足
满足 ![]() =2
=2 ![]() ﹣
﹣ ![]() ,
, ![]() =k
=k ![]() +
+ ![]() ,给出以下结论:
,给出以下结论:
①若 ![]() 与
与 ![]() 不共线,
不共线, ![]() 与
与 ![]() 共线,则k=﹣2;
共线,则k=﹣2;
②若 ![]() 与
与 ![]() 不共线,
不共线, ![]() 与
与 ![]() 共线,则k=2;
共线,则k=2;
③存在实数k,使得 ![]() 与
与 ![]() 不共线,
不共线, ![]() 与
与 ![]() 共线;
共线;
④不存在实数k,使得 ![]() 与
与 ![]() 不共线,
不共线, ![]() 与
与 ![]() 共线.
共线.
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为
的短轴长为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于左、右顶点
上异于左、右顶点![]() 的一点.
的一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,证明:点
,证明:点![]() 关于直线
关于直线![]() 的对称点在直线
的对称点在直线![]() 上.
上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com