Question

（本题满分14分）已知椭圆的中心为坐标原点，短轴长为2，一条准线方程为l：．

⑴ 求椭圆的标准方程；⑵ 设O为坐标原点，F是椭圆的右焦点，点M是直线l上的动点，过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值．

Answer 1

（本题满分14分）

已知椭圆的中心为坐标原点，短轴长为2，一条准线方程为l：．

⑴ 求椭圆的标准方程；

⑵ 设O为坐标原点，F是椭圆的右焦点，点M是直线l上的动点，过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值．

解：⑴∵椭圆C的短轴长为2，椭圆C的一条准线为l：，

∴不妨设椭圆C的方程为．（2分）∴，（ 4分）即．（5分）

∴椭圆C的方程为．（6分）

    ⑵ F（1，0），右准线为l：， 设，

     则直线FN的斜率为，直线ON的斜率为，（8分）

     ∵FN⊥OM，∴直线OM的斜率为，（9分）

    ∴直线OM的方程为：，点M的坐标为．（11分）

    ∴直线MN的斜率为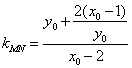．（12分）

    ∵MN⊥ON，∴，    ∴，

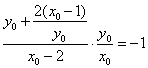∴，即．（13分）∴为定值．（14分）

说明:若学生用平面几何知识（圆幂定理或相似形均可）也得分，设垂足为P，准线l与x轴交于Q，则有，又，所以为定值．