
【题目】已知函数f(x)=mex+x2+nx,{x|f(x)=0}={x|f(f(x))=0}≠,则m+n的取值范围为( )
A.(0,4)
B.[0,4)
C.[0,4]
D.(4,+∞)
【答案】B
【解析】解:设x1∈{x|f(x)=0}={x|f(f(x))=0},
∴f(x1)=f(f(x1))=0,
∴f(0)=0,
即f(0)=m=0,
故m=0;
故f(x)=x2+nx,
f(f(x))=(x2+nx)(x2+nx+n)=0,
当n=0时,成立;
当n≠0时,0,﹣n不是x2+nx+n=0的根,
故△=n2﹣4n<0,
解得:0<n<4;
综上所述,0≤n+m<4;
故选:B.
【考点精析】认真审题,首先需要了解集合的表示方法-特定字母法(①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合.③描述法:{![]() |
|![]() 具有的性质},其中
具有的性质},其中![]() 为集合的代表元素.④图示法:用数轴或韦恩图来表示集合).
为集合的代表元素.④图示法:用数轴或韦恩图来表示集合).


科目:高中数学 来源: 题型:
【题目】以下命题:
①“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
②命题“若 ![]() ,则
,则 ![]() ”的逆否命题为“若
”的逆否命题为“若 ![]() ,则
,则 ![]() ”;
”;
③对于命题 ![]() :
: ![]() ,使得
,使得 ![]() ,则
,则 ![]() :
: ![]() ,均有
,均有 ![]() ;
;
④若 “![]() 为假命题,则
为假命题,则 ![]() ,
, ![]() 均为假命题;
均为假命题;
其中正确命题的序号为_______________(把所有正确命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是  (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图给出了一个程序框图,其作用是输入x的值,输出相应的y值.若要使输入的x值与输出的y值相等,则这样的x值有( ) 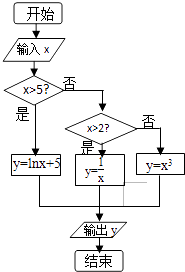
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,经过点
中,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() 和
和![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)设椭圆与![]() 轴正半轴、
轴正半轴、![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,是否存在常数
,是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD
为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD![]() 平面PBC=
平面PBC=![]() .
.

(1)求证:BC∥![]() ;
;
(2)MN与平面PAD是否平行?试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2 , a4的等差中项.
(1)求数列{an}的通项公式;
(2)设bn=anlog2an , 其前n项和为Sn , 若(n﹣1)2≤m(Sn﹣n﹣1)对于n≥2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x+3|<2x+1的解集为{x|x>m}.
(1)求m的值;
(2)设关于x的方程|x﹣t|+|x+ ![]() |=m(t≠0)有解,求实数t的值.
|=m(t≠0)有解,求实数t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若向量 ![]() ,其中ω>0,记函数
,其中ω>0,记函数 ![]() ,若函数f(x)的图象与直线y=m(m为常数)相切,并且切点的横坐标依次成公差为π的等差数列.
,若函数f(x)的图象与直线y=m(m为常数)相切,并且切点的横坐标依次成公差为π的等差数列.
(1)求f(x)的表达式及m的值;
(2)将函数y=f(x)的图象向左平移 ![]() ,得到y=g(x)的图象,当
,得到y=g(x)的图象,当 ![]() 时,y=g(x)与y=cosα的交点横坐标成等比数列,求钝角α的值.
时,y=g(x)与y=cosα的交点横坐标成等比数列,求钝角α的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com