
【题目】如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.

求证:(1)A1B1∥平面DEC1;
(2)BE⊥C1E.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由题意结合几何体的空间结构特征和线面平行的判定定理即可证得题中的结论;
(2)由题意首先证得线面垂直,然后结合线面垂直证明线线垂直即可.
(1)因为D,E分别为BC,AC的中点,
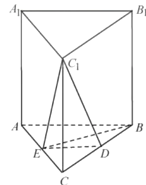
所以ED∥AB.
在直三棱柱ABC-A1B1C1中,AB∥A1B1,
所以A1B1∥ED.
又因为ED平面DEC1,A1B1![]() 平面DEC1,
平面DEC1,
所以A1B1∥平面DEC1.
(2)因为AB=BC,E为AC的中点,所以BE⊥AC.
因为三棱柱ABC-A1B1C1是直棱柱,所以CC1⊥平面ABC.
又因为BE平面ABC,所以CC1⊥BE.
因为C1C平面A1ACC1,AC平面A1ACC1,C1C∩AC=C,
所以BE⊥平面A1ACC1.
因为C1E平面A1ACC1,所以BE⊥C1E.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】2016年1月1日,我国实行全面二孩政策,同时也对妇幼保健工作提出了更高的要求.某城市实行网格化管理,该市妇联在网格1与网格2两个区域内随机抽取12个刚满8个月的婴儿的体重信息,体重分布数据的茎叶图如图所示(单位:斤,2斤![]() 1千克),体重不超过
1千克),体重不超过![]() 千克的为合格.
千克的为合格.

(1)从网格1与网格2分别随机抽取2个婴儿,求网格1至少有一个婴儿体重合格且网格2至少有一个婴儿体重合格的概率;
(2)妇联从网格1内8个婴儿中随机抽取4个进行抽检,若至少2个婴儿合格,则抽检通过,若至少3个合格,则抽检为良好,求网格1在抽检通过的条件下,获得抽检为良好的概率;
(3)若从网格1与网格2内12个婴儿中随机抽取2个,用![]() 表示网格2内婴儿的个数,求
表示网格2内婴儿的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网上购物逐步走进大学生活,某大学学生宿舍4人积极参加网购,大家约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商城购物,且参加者必须从淘宝网和京东商城选择一家购物.
(1)求这4个人中恰有1人去淘宝网购物的概率;
(2)用![]() ,
,![]() 分别表示这4个人中去淘宝网和京东商城购物的人数,记
分别表示这4个人中去淘宝网和京东商城购物的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义在R上的奇函数,且当x≥0时,f(x)=-x2+ax.
(1)若a=-2,求函数f(x)的解析式;
(2)若函数f(x)为R上的单调减函数,
①求a的取值范围;
②若对任意实数m,f(m-1)+f(m2+t)<0恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市为调查会员某年度上半年的消费情况制作了有奖调查问卷发放给所有会员,并从参与调查的会员中随机抽取![]() 名了解情况并给予物质奖励.调查发现抽取的
名了解情况并给予物质奖励.调查发现抽取的![]() 名会员消费金额(单位:万元)都在区间
名会员消费金额(单位:万元)都在区间![]() 内,调查结果按消费金额分成
内,调查结果按消费金额分成![]() 组,制作成如下的频率分布直方图.
组,制作成如下的频率分布直方图.
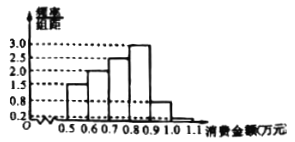
(1)求该![]() 名会员上半年消费金额的平均值与中位数;(以各区间的中点值代表该区间的均值)
名会员上半年消费金额的平均值与中位数;(以各区间的中点值代表该区间的均值)
(2)现采用分层抽样的方式从前![]() 组中选取
组中选取![]() 人进行消费爱好调查,然后再从前
人进行消费爱好调查,然后再从前![]() 组选取的人中随机选
组选取的人中随机选![]() 人,求这
人,求这![]() 人都来自第
人都来自第![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于等差数列和等比数列的叙述正确的是( )
A.若非常数列![]() 为等差数列,则
为等差数列,则![]() 也可能是等差数列
也可能是等差数列
B.若非常数列![]() 为等比数列,则
为等比数列,则![]() 不可能是等差数列
不可能是等差数列
C.若数列![]() 的前n项和
的前n项和![]()
![]() ,则数列
,则数列![]() 可能是等差数列
可能是等差数列
D.若等差数列![]() 的前n项和
的前n项和![]() 有最大值,则公差d可能大于零
有最大值,则公差d可能大于零
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为
的长轴长为![]() ,
, ![]() ,
, ![]() 是其长轴顶点,
是其长轴顶点, ![]() 是椭圆上异于
是椭圆上异于![]() ,
, ![]() 的动点,且
的动点,且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
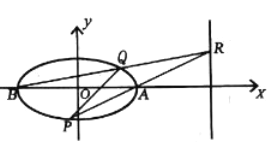
(2)如图,若动点![]() 在直线
在直线![]() 上,直线
上,直线![]() ,
, ![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
, ![]() 两点.请问:直线
两点.请问:直线![]() 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com