【题目】已知函数
．
（1）将函数
的图像向右平移
个单位得到函数
的图像，若
，求函数
的值域；
（2）已知
，分别为
中角
的对边，且满足
，求
的面积．
【答案】（1）
；（2）
.
【解析】
试题分析：化简
，（1）平移得
，又
当
时，
；当
时，
所求值域为；（2）由正弦定理得：
，由
．
试题解析：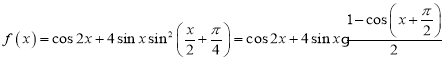
．．．．．．．．．．1分
=．．．．．．．．．．．．．．．．．．．．．．3分
（1）平移可得，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分
∵
，∴，．．．．．．．．．．．．．．．．．．．．5分
当时，；当时，．．．．．．．．．．．．．．．．6分
∴所求值域为．．．．．．．．．．．．．．．7分
（2）由已知
及正弦定理得：．．．．．．．．．．．．．．．．．． ８分
∴，∵
，∴，由得，又
，
∴………………………………………10分
由正弦定理得：，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．11分
∴
．．．．．．．．．．．．．．．． 12分
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】选修
：坐标系与参数方程
已知曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l过点M（1，0），倾斜角为
．
（Ⅰ）求曲线C的直角坐标方程与直线l的参数方程；
（Ⅱ）若曲线C经过伸缩变换
后得到曲线C′，且直线l与曲线C′交于A，B两点，求|MA|+|MB|．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知定义在R上的函数
是奇函数,函数
的定义域为
.
（1）求
的值；
（2）若
在
上单调递减，根据单调性的定义求实数
的取值范围；
（3）在(2)的条件下，若函数
在区间
上有且仅有两个不同的零点，求实数的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知(x，y)在映射f的作用下的像是(x＋y，xy)．
(1)求(－2,3)在f作用下的像；
(2)若在f作用下的像是(2，－3)，求它的原像．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从某企业生产的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：
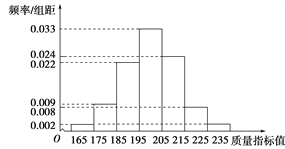
(1)求这500件产品质量指标值的样本平均数
和样本方差s2(同一组中的数据用该组区间的中点值作代表)；
(2)由直方图可以认为，这种产品的质量指标值Z服从正态分布N(μ，σ2)，其中μ近似为样本平均数
，σ2近似为样本方差s2.
(ⅰ)利用该正态分布，求P(187.8<Z<212.2)；
(ⅱ)某用户从该企业购买了100件这种产品，记X表示这100件产品中质量指标值位于区间(187.8，212.2)的产品件数.利用(ⅰ)的结果，求E(X).
附： 
≈12.2.若Z～N(μ，σ2)，则P(μ－σ<Z<μ＋σ)＝0.682 6，P(μ－2σ<Z<μ＋2σ)＝0.954 4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
