
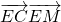 的取值范围是________.
的取值范围是________. ,
, ]
]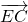 、
、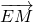 关于x的坐标形式,从而得到
关于x的坐标形式,从而得到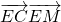 =x2-2x+
=x2-2x+ ,最后结合x的取值范围和二次函数的性质,即可得到
,最后结合x的取值范围和二次函数的性质,即可得到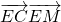 的取值范围.
的取值范围.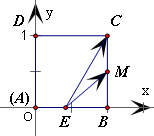
 ),设E(x,0)(0≤x≤1)
),设E(x,0)(0≤x≤1)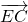 =(1-x,1),
=(1-x,1),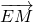 =(1-x,
=(1-x, )
)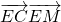 =(1-x)(1-x)+1×
=(1-x)(1-x)+1× =x2-2x+
=x2-2x+
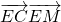 有最小值为
有最小值为 ;当x=0时,
;当x=0时,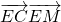 有最大值为
有最大值为
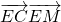 的取值范围是[
的取值范围是[ ,
, ]
] ,
, ]
]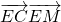 的最大、最小值.着重考查了正方形的性质、平面向量数量积的定义与坐标运算等知识,属于基础题.
的最大、最小值.着重考查了正方形的性质、平面向量数量积的定义与坐标运算等知识,属于基础题. 

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
 如图,四边形ABCD是一个边长为1的正方形,△MPN是正方形的一个内接正三角形,且MN∥AB,若向正方形内部随机投入一个质点,则质点恰好落在△MPN的概率为( )
如图,四边形ABCD是一个边长为1的正方形,△MPN是正方形的一个内接正三角形,且MN∥AB,若向正方形内部随机投入一个质点,则质点恰好落在△MPN的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
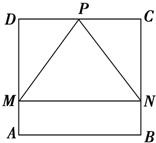
 如图,两个边长为1的正方形ABCD与ABEF相交于AB,∠EBC=90°,M,N分别是BD,AE上的点,且AN=DM.
如图,两个边长为1的正方形ABCD与ABEF相交于AB,∠EBC=90°,M,N分别是BD,AE上的点,且AN=DM.查看答案和解析>>
科目:高中数学 来源: 题型:
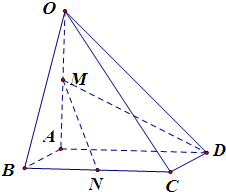 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题查看答案和解析>>
科目:高中数学 来源: 题型:
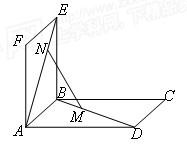
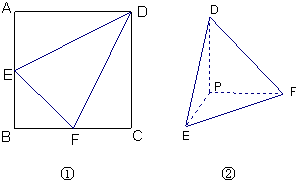 (2011•揭阳一模)如图①边长为1的正方形ABCD中,点E、F分别为AB、BC的中点,将△BEF剪去,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点P得一三棱锥如图②示.
(2011•揭阳一模)如图①边长为1的正方形ABCD中,点E、F分别为AB、BC的中点,将△BEF剪去,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点P得一三棱锥如图②示.查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com