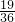Question

设b、c分别是先后抛掷一枚骰子得到的点数，
（1）求方程x²+bx+c=0有实根的概率；
（2）求在先后两次出现的点数中有5的条件下，方程x²+bx+c=0有实根的概率．

Answer 1

解：（1）由题意知本题是一个等可能事件的概率，
试验发生包含的事件数是6×6=36种结果，
方程x²+bx+c=0有实根要满足b²-4c≥0，
当b=2，c=1
b=3，c=1，2
b=4，c=1，2，3，4
b=5，c=1，2，3，4，5，6，
b=6，c=1，2，3，4，5，6
综上可知共有1+2+4+6+6=19种结果
∴要求的概率是
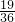
（2）本题可以按照等可能事件的概率来考虑
试验发生包含的事件数5+6=11，
满足条件的事件由上一问可以看出有6+1=7种结果
∴满足条件的概率是
分析：（1）本题是一个等可能事件的概率，试验发生包含的事件数是6×6=36种结果，方程x²+bx+c=0有实根要满足判别式不小于0，列举出结果．
（2）本题可以按照等可能事件的概率来考虑，试验发生包含的事件数5+6，满足条件的事件由上一问可以看出有6+1种结果，写出概率．
点评：本题考查等可能事件的概率，在解题过程中主要应用列举法来列举出所有的满足条件的事件数，这是本题的精华部分．