练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．冶炼某种金属可以用旧设备和改造后的新设备，为了检验用这两种设备生产的产品中所含杂质的关系，调查结果如下表所示．
    杂质高杂质低
    旧设备37121
    新设备22202
    根据以上数据，则（　　）
    A．含杂质的高低与设备改造有关B．含杂质的高低与设备改造无关
    C．设备是否改造决定含杂质的高低D．以上答案都不对

    分析 根据所给的数据写出列联表，把列联表的数据代入观测值的公式，求出两个变量之间的观测值，把观测值同临界值表中的数据进行比较，得到有99%的把握认为含杂质的高低与设备是否改造是有关的．

    解答 解：由已知数据得到如下2×2列联表

    杂质高杂质低合计
    旧设备37121158
    新设备22202224
    合计59323382
    由公式κ2=$\frac{382×（37×202-22×121）^{2}}{59×224×59×323}$≈13.11，
    由于13.11＞6.635，故有99%的把握认为含杂质的高低与设备是否改造是有关的．

    点评 本题考查独立性检验，考查写出列联表，这是一个基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

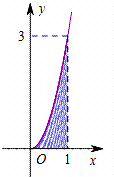    7．已知函数f（x）的部分图象如图所示．向图中的矩形区域随机投出100粒豆子，记下落入阴影区域的豆子数．通过10次这样的试验，算得落入阴影区域的豆子的平均数约为33，由此可估计${∫}_{0}^{1}$f（x）dx的值约为（　　）
    A．$\frac{99}{100}$B．$\frac{3}{10}$C．$\frac{9}{10}$D．$\frac{10}{11}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知关于x的方程x2-（bcosA）x+acosB=0的两根之积等于两根之和，且边a，b为△ABC的两内角A，B所对的边，则△ABC是（　　）
    A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．若数列{an}的通项公式是an=2×（-3）n，则该数列是（　　）
    A．公比为-3的等比数列B．公比为2的等比数列
    C．公比为3的等比数列D．首项为2的等比数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知 {an}，{bn}均为等差数列，前n项和分别为 Sn，Tn．
    （1）若对 n∈N*，有 $\frac{S_n}{T_n}=\frac{31n+101}{n+3}$，求 $\frac{a_n}{b_n}$的最大值．
    （2）若平面内三个不共线向量 $\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}$满足 $\overrightarrow{OC}={a_3}\overrightarrow{OA}+{a_{15}}\overrightarrow{OB}$，且A，B，C三点共线．是否存在正整数n，使 Sn为定值？若存在，请求出此定值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

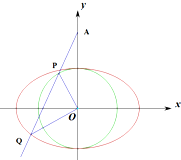    2．如图，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，短轴端点在圆O：x2+y2=1上
    （1）求椭圆C的标准方程
    （2）设过点A（0，2）的动直线l与圆O有公共点，且与椭圆C相交于P，Q两点，求△OPQ面积的最大值及取得最大值时l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知命题p：?x∈R，2x＜3x；命题q：?x∈R，使得log0.5x=x，则下列命题中为真命题的是（　　）
    A．p∧qB．￢p∧qC．p∧￢qD．￢p∧￢q

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．若$a={log_{\frac{1}{3}}}2，b={2^{\frac{1}{3}}}，c={（\frac{1}{3}）^{-\frac{1}{2}}}$，则（　　）
    A．a＜b＜cB．b＜c＜aC．c＜a＜bD．c＜b＜a

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知a=2+$\sqrt{3}$，b=1+$\sqrt{6}$，c=$\sqrt{2}$+$\sqrt{5}$，则a，b，c的大小关系为（　　）
    A．a＞b＞cB．c＞a＞bC．a＞c＞bD．c＞b＞a

    查看答案和解析>>

    同步练习册答案