
【题目】在![]() 中,内角A,B,C所对的边长分别是a,b,c.
中,内角A,B,C所对的边长分别是a,b,c.
(1)若![]() ,
,![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,试判断△ABC的形状.
,试判断△ABC的形状.
【答案】(1) a=2,b=2 (2)等腰三角形或直角三角形
【解析】
试题分析:(1)根据余弦定理,得![]() ,再由面积正弦定理得
,再由面积正弦定理得![]() ,两式联解可得到a,b的值;
,两式联解可得到a,b的值;
(2)根据三角形内角和定理,得到sinC=sin(A+B),代入已知等式,展开化简合并,得sinBcosA=sinAcosA,最后讨论当cosA=0时与当cosA≠0时,分别对△ABC的形状的形状加以判断,可以得到结论.
试题解析:(1) ∵c=2, ![]()
![]() ,
,
∴由余弦定理c2=a2+b2-2abcosC得a2+b2-ab=4.
又∵△ABC的面积为![]() ,∴
,∴![]() absinC=
absinC=![]() ,∴ab=4.
,∴ab=4.
联立方程组![]() 解得a=2,b=2.
解得a=2,b=2.
(2)由sinC+sin(B-A)=sin2A,得sin(A+B)+sin(B-A)=2sinAcosA,
即2sinBcosA=2sinAcosA,
∴cosA·(sinA-sinB)=0,∴cosA=0或sinA-sinB=0,
当cosA=0时,∵0<A<π,∴A=![]() ,△ABC为直角三角形;
,△ABC为直角三角形;
当sinA-sinB=0时,得sinB=sinA,由正弦定理得a=b,
即△ABC为等腰三角形.
∴△ABC为等腰三角形或直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了了解我市参加2018年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成![]() 六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
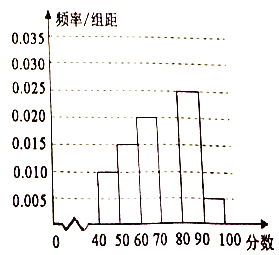
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试成绩的众数、均值;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要所少分?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
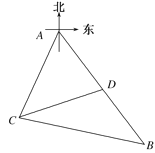
【题目】某观测站![]() 在目标
在目标![]() 的南偏西
的南偏西![]() 方向,从
方向,从![]() 出发有一条南偏东
出发有一条南偏东![]() 走向的公路,在
走向的公路,在![]() 处测得与
处测得与![]() 相距
相距![]() 的公路
的公路![]() 处有一个人正沿着此公路向
处有一个人正沿着此公路向![]() 走去,走
走去,走![]() 到达
到达![]() ,此时测得
,此时测得![]() 距离为
距离为![]() ,若此人必须在
,若此人必须在![]() 分钟内从
分钟内从![]() 处到达
处到达![]() 处,则此人的最小速度为( )
处,则此人的最小速度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,仅在北京地区每天就有500万单快递等待派送,近5万多名快递员奔跑在一线,快递网点人员流动性也较强,各快递公司需要经常招聘快递员,保证业务的正常开展.下面是50天内甲、乙两家快递公司的快递员每天送货单数统计表:
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 6 | 14 | 24 | 6 | |
已知这两家快递公司的快递员日工资方案分别为:甲公司规定底薪![]() 元,每单抽成
元,每单抽成![]() 元;乙公司规定底薪
元;乙公司规定底薪![]() 元,每日前
元,每日前![]() 单无抽成,超过
单无抽成,超过![]() 单的部分每单抽成
单的部分每单抽成![]() 元.
元.
(1)分别求甲、乙快递公司的快递员的日工资![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
(2)小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作,如果仅从日收入的角度考虑,以这50天的送货单数为样本,将频率视为概率,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 过点
过点 ,离心率为
,离心率为![]() .
.![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,
的上、下顶点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的一点.
的一点.

(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求
,求![]() 的面积;
的面积;
(3)过点![]() 作斜率为
作斜率为![]() 的直线分别交椭圆
的直线分别交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,且点
,且点![]() 在线段
在线段![]() 上(不包括端点
上(不包括端点![]() ),直线
),直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1,2,3,4,5,6,7,8,9这9个数字中任取两个数,分别有下列事件:
①恰有一个是奇数和恰有一个是偶数;
②至少有一个是奇数和两个数都是奇数;
③至少有一个是奇数和两个数都是偶数;
④至少有一个是奇数和至少有一个是偶数.
其中,为互斥事件的是( )
A.①B.②④C.③D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义域为R的奇函数,当x<0时,![]() .
.
(1)求f(2)的值;
(2)用定义法判断y=f(x)在区间(-∞,0)上的单调性.
(3)求![]() 的解析式
的解析式
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中, 曲线
中, 曲线![]() 的参数方程为
的参数方程为![]() 为参数) ;在以原点
为参数) ;在以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中, 曲线
轴的正半轴为极轴的极坐标系中, 曲线![]() 的极坐标参数方程为
的极坐标参数方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() ,
,![]() 的交点分别为
的交点分别为![]() (
(![]() 异于原点). 当斜率
异于原点). 当斜率![]() 时, 求
时, 求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com