
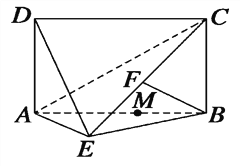
【题目】如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,
BF⊥平面ACE,且点F在CE上.
(1)求证:AE⊥BE;
(2)求三棱锥D—AEC的体积;
(3)设点M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,
使得MN∥平面DAE.
【答案】(1)![]() ;(2)
;(2)![]() .(3)点N为线段CE上靠近点C的一个三等分点
.(3)点N为线段CE上靠近点C的一个三等分点
【解析】试题分析:(1)先证明![]() ,可得AE⊥平面BCE,由此能证明
,可得AE⊥平面BCE,由此能证明![]() ;(2)由
;(2)由![]() ,能求出三棱锥
,能求出三棱锥![]() 的体积;(3)过点
的体积;(3)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,推导出
,推导出![]() 平面
平面![]() ,由此能求出当点
,由此能求出当点![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的一个三等分点时,
的一个三等分点时,![]() 平面
平面![]() .
.
试题解析:(1)证明 由AD⊥平面ABE及AD∥BC,
得BC⊥平面ABE,BC⊥AE,
而BF⊥平面ACE,所以BF⊥AE,
又BC∩BF=B,所以AE⊥平面BCE,
又BE平面BCE,故AE⊥BE.
在△ABE中,过点E作EH⊥AB于点H,
则EH⊥平面ACD.
由已知及(1)得EH=![]() AB=
AB=![]() ,S△ADC=2
,S△ADC=2![]() .
.
故VD—AEC=VE—ADC=![]() ×2
×2![]() ×
×![]() =
=![]() .(10分)
.(10分)
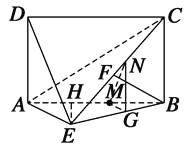
(3)解:在△ABE中,过点M作MG∥AE交BE于点G,在△BEC中过点G作GN∥BC交EC于点N,
连结MN,则由![]() =
=![]() =
=![]() =
=![]() ,得CN=
,得CN=![]() CE.
CE.
由MG∥AE,AE平面ADE,
MG平面ADE,则MG∥平面ADE.(12分)
再由GN∥BC,BC∥AD,AD平面ADE,GN平面ADE,
得GN∥平面ADE,所以平面MGN∥平面ADE.
又MN平面MGN,则MN∥平面ADE.(15分)
故当点N为线段CE上靠近点C的一个三等分点时,
MN∥平面ADE.
【方法点晴】本题主要考查线面平行的判定定理、直线和平面成的角的定义及求法、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合 计 | M | N |
(1)求出表中![]() 所表示的数分别是多少?
所表示的数分别是多少?
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?由直方图确定此组数据中位数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点![]() ,且与直线
,且与直线![]() 相切.
相切.
(1)求动圆圆心的轨迹![]() 的方程;
的方程;
(2)过(1)中轨迹![]() 上的点
上的点![]() 作两条直线分别与轨迹
作两条直线分别与轨迹![]() 相交于
相交于![]() 两点,试探究:当直线
两点,试探究:当直线![]() 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线![]() 的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为坐标原点,
为坐标原点,![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,生产1吨A种产品需要煤4吨、电18千瓦;生产1吨B种产品需要煤1吨、电15千瓦。现因条件限制,该企业仅有煤10吨,并且供电局只能供电66千瓦,若生产1吨A种产品的利润为10000元;生产1吨B种产品的利润是5000元,试问该企业如何安排生产,才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为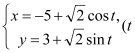 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 是圆
是圆![]() 上任一点,求
上任一点,求![]() 两点的极坐标和
两点的极坐标和![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com