
【题目】已知数列{an}是各项均为正整数的等差数列,公差d∈N* , 且{an}中任意两项之和也是该数列中的一项.
(1)若a1=4,则d的取值集合为;
(2)若a1=2m(m∈N*),则d的所有可能取值的和为 .
【答案】
(1){1,2,4}
(2)2m+1﹣1
【解析】解:由题意可得,ap+aq=ak , 其中p、q、k∈N* , 由等差数列的通向公式可得a1+(p﹣1)d+a1+(q﹣1)d=a1+(k﹣1),
整理得d= ![]() ,
,
1)若a1=4,则d= ![]() ,
,
∵p、q、k∈N* , 公差d∈N* ,
∴k﹣p﹣q+1∈N* ,
∴d=1,2,4,
故d的取值集合为 {1,2,4};
2)若a1=2m(m∈N*),则d= ![]() ,
,
∵p、q、k∈N* , 公差d∈N* ,
∴k﹣p﹣q+1∈N* ,
∴d=1,2,4,…,2m ,
∴d的所有可能取值的和为1+2+4+…+2m= ![]() =2m+1﹣1,
=2m+1﹣1,
所以答案是(1){1,2,4},(2)2m+1﹣1.
【考点精析】利用等比数列的前n项和公式和等差数列的性质对题目进行判断即可得到答案,需要熟知前![]() 项和公式:
项和公式: ;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列.
;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】在数列![]() 中,已知
中,已知![]() ,且对于任意正整数n都有
,且对于任意正整数n都有![]() .
.
(1)令![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)求![]() 的通项公式;
的通项公式;
(3)设![]() 是一个正数,无论
是一个正数,无论![]() 为何值,都有一个正整数
为何值,都有一个正整数![]() 使
使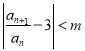 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级共有学生![]() 名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为
名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为![]() 分)进行统计,绘制出如下尚未完成的频率分布表:
分)进行统计,绘制出如下尚未完成的频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
| |
| ||
|
|
(1)补充完整题中的频率分布表;
(2)若成绩在![]() 为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于正整数集合![]() ,如果去掉其中任意一个元素
,如果去掉其中任意一个元素![]() 之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合
之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合![]() 为“和谐集”.
为“和谐集”.
(![]() )判断集合
)判断集合![]() 是否是“和谐集”(不必写过程).
是否是“和谐集”(不必写过程).
(![]() )请写出一个只含有
)请写出一个只含有![]() 个元素的“和谐集”,并证明此集合为“和谐集”.
个元素的“和谐集”,并证明此集合为“和谐集”.
(![]() )当
)当![]() 时,集合
时,集合![]() ,求证:集合
,求证:集合![]() 不是“和谐集”.
不是“和谐集”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l过点M(3,4),其倾斜角为45°,圆C的参数方程为 ![]() .再以原点为极点,以x正半轴为极轴建立极坐标系,并使得它与直角坐标系xoy有相同的长度单位.
.再以原点为极点,以x正半轴为极轴建立极坐标系,并使得它与直角坐标系xoy有相同的长度单位.
(1)求圆C的极坐标方程;
(2)设圆C与直线l交于点A、B,求|MA||MB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是一个容量为20的样本数据分组后的频率分布表:
分组 |
|
|
|
| ||
频数 | 4 | 2 | 6 | 8 | ||
(1)请估计样本的平均数;
(2)以频率估计概率,若样本的容量为2000,求在分组![]() 中的频数;
中的频数;
(3)若从数据在分组![]() 与分组
与分组![]() 的样本中随机抽取2个,求恰有1个样本落在分组
的样本中随机抽取2个,求恰有1个样本落在分组![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面凸四边形![]() 中(凸四边形指没有角度数大于
中(凸四边形指没有角度数大于![]() 的四边形),
的四边形),![]() .
.

(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)已知![]() ,记四边形
,记四边形![]() 的面积为
的面积为![]() .
.
① 求![]() 的最大值;
的最大值;
② 若对于常数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.(直接写结果,不需要过程)
的取值范围.(直接写结果,不需要过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+mx+n(m,n∈R)满足f(0)=f(1),且方程x=f(x)有两个相等的实数根.
(1)求函数f(x)的解析式;
(2)当x∈[0,3]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为![]() ,半径为1,该纸片上的等边三角形
,半径为1,该纸片上的等边三角形![]() 的中心为
的中心为![]() .
.![]() 、
、![]() 、
、![]() 为圆
为圆![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() 分别是以
分别是以![]() ,
,![]() ,
,![]() 为底边的等腰三角形.沿虚线剪开后,分别以
为底边的等腰三角形.沿虚线剪开后,分别以![]() ,
,![]() ,
,![]() 为折痕折起
为折痕折起![]() ,
,![]() ,
,![]() ,使得
,使得![]() 、
、![]() 、
、![]() 重合,得到三棱锥.当
重合,得到三棱锥.当![]() 的边长变化时,所得三棱锥体积的最大值为__________.
的边长变化时,所得三棱锥体积的最大值为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com