
【题目】下列判断正确的是 (把正确的序号都填上).
①若f(x)=ax2+(2a+b)x+2 (其中x∈[2a-1,a+4])是偶函数,则实数b=2;
②若函数![]() 在区间
在区间![]() 上递增,在区间
上递增,在区间![]() 上也递增,则函数
上也递增,则函数![]() 必在
必在![]() 上递增;
上递增;
③f(x)表示-2x+2与-2x2+4x+2中的较小者,则函数f(x)的最大值为1;
④已知f(x)是定义在R上的不恒为零的函数,且对任意的x、y∈R都满足f(x·y)=x·f(y)+y·f(x),则f(x)是奇函数.Ks
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx与g(x)=log4(a2x﹣![]() a),其中f(x)是偶函数.
a),其中f(x)是偶函数.
(1)求实数k的值;
(2)求函数g(x)的定义域;
(3)若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为F1 , F2 , 离心率为
的左、右焦点分别为F1 , F2 , 离心率为 ![]() ,短轴上的两个顶点为A,B(A在B的上方),且四边形AF1BF2的面积为8.
,短轴上的两个顶点为A,B(A在B的上方),且四边形AF1BF2的面积为8.
(1)求椭圆C的方程;
(2)设动直线y=kx+4与椭圆C交于不同的两点M,N,直线y=1与直线BM交于点G,求证:A,G,N三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为![]() 的半圆形(
的半圆形(![]() 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料![]() ,其中
,其中![]() 在直径上,点
在直径上,点![]() 在圆周上.
在圆周上.
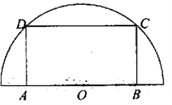
(1)设![]() ,将矩形
,将矩形![]() 的面积
的面积![]() 表示成
表示成![]() 的函数,并写出其定义域;
的函数,并写出其定义域;
(2)怎样截取,才能使矩形材料![]() 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数h(x)=ax3+bx2+cx+d(a≠0)图象的对称中心为M(x0 , h(x0)),记函数h(x)的导函数为g(x),则有g′(x0)=0,设函数f(x)=x3﹣3x2+2,则f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(
)+f( ![]() )= .
)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1 , AB⊥AN,CB=BA=AN= ![]() BB1 .
BB1 . 
(1)求证:BN⊥平面C1B1N;
(2)求二面角C﹣C1N﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1= ![]() (n∈N*).
(n∈N*).
(1)求证:{ ![]() +
+ ![]() }为等比数列,并求{an}的通项公式an;
}为等比数列,并求{an}的通项公式an;
(2)数列{bn}满足bn=(3n﹣1) ![]() an , 求数列{bn}的前n项和Tn .
an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com