
【题目】已知函数f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1
(1)求f(1)、f( ![]() )的值;
)的值;
(2)若满足f(x)+f(x﹣8)≤2,求x的取值范围.
【答案】
(1)解:令x=y=1得:f(11)=f(1)+f(1),
∴f(1)=0;
令y= ![]() ,则f(x
,则f(x ![]() )=f(x)+f(
)=f(x)+f( ![]() )=f(1)=0,
)=f(1)=0,
∵f(3)=1,
∴f( ![]() )=﹣f(3)=﹣1
)=﹣f(3)=﹣1
(2)解:∵f(9)=f(3)+f(3)=2,
∴f(x)+f(x﹣8)≤2f[x(x﹣8)]≤f(9),
而函数f(x)在定义域(0,+∞)上为增函数,
∴ 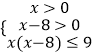 ,
,
解得:8<x≤9,
∴x的取值范围是(8,9]
【解析】(1)令x=y=1易得f(1)=0;令y= ![]() ,可得f(x)+f(
,可得f(x)+f( ![]() )=0,于是由f(3)=1可求得f(
)=0,于是由f(3)=1可求得f( ![]() )的值;(2)由f(x)+f(x﹣8)<2,知f(x)+f(x﹣8)=f[x(x﹣8)]<f(9),再由函数f(x)在定义域(0,+∞)上为增函数,能求出原不等式的解集.
)的值;(2)由f(x)+f(x﹣8)<2,知f(x)+f(x﹣8)=f[x(x﹣8)]<f(9),再由函数f(x)在定义域(0,+∞)上为增函数,能求出原不等式的解集.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的中心为O,四边形ODEF为矩形,平面ODEF![]() 平面ABCD,DE=DA=DB=2
平面ABCD,DE=DA=DB=2
(I)若G为DC的中点,求证:EG//平面BCF;
(II)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y= ![]() 的定义域为M,那么( )
的定义域为M,那么( )
A.{x|x>﹣1且x≠0}
B.{x|x>﹣1}
C.M={x|x<﹣1或x>0}
D.M={x|x<﹣1或﹣1<x<0或x>0}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() +aln x(a≠0,a∈R).
+aln x(a≠0,a∈R).
(1)若a=1,求函数f(x)的极值和单调区间;
(2)若在区间(0,e]上至少存在一点x0,使得f(x0)<0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax2﹣(2a+1)x+2lnx(a≥0)
ax2﹣(2a+1)x+2lnx(a≥0)
(1)当a=0时,求f(x)的单调区间;
(2)求y=f(x)在区间(0,2]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=x3+ax2+bx+1的导函数f′(x)满足f′(x)=2a,f′(2)=﹣b,
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设g(x)=f′(x)ex , 求函数g(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 
(1)当x≤0时,解不等式f(x)≥﹣1;
(2)写出该函数的单调区间;
(3)若函数g(x)=f(x)﹣m恰有3个不同零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() 是定义在(﹣∞,+∞)上的奇函数,且f(
是定义在(﹣∞,+∞)上的奇函数,且f( ![]() )=
)= ![]() .
.
(1)求实数a、b,并确定函数f(x)的解析式;
(2)判断f(x)在(﹣1,1)上的单调性,并用定义证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com