
【题目】已知函数![]() ,m∈R
,m∈R
(1)讨论f(x)的单调性;
(2)若m∈(-1,0),证明:对任意的x1,x2∈[1,1-m],4f(x1)+x2<5.
【答案】(1)见解析;(2)见解析
【解析】
(1)求函数的导数,结合函数单调性和导数之间的关系进行判断即可.
(2)将不等式进行转化,构造函数g(x)=-![]() x+
x+![]() ,则不等式转化为最值问题进行求解即可.
,则不等式转化为最值问题进行求解即可.
解:(1)![]()
①当1>1-m,即m>0时,(-∞,1-m)和(1,+∞)上f′(x)<0,f(x)单调减;(1-m,1)上f′(x)>0,f(x)单调增
②当1=1-m,即m=0时,(-∞,+∞)上f′(x)<0,f(x)单调减
③当1<1-m,即m<0时,(-∞,1)和(1-m,+∞)上f′(x)<0,f(x)单调减;(1,1-m)上f′(x)>0,f(x)单调增
(2)对任意的x1,x2∈[1,1-m],4f(x1)+x2<5可转化为![]() ,
,
设g(x)=-![]() x+
x+![]() ,则问题等价于x1,x2∈[1,1-m],f(x)max<g(x)min
,则问题等价于x1,x2∈[1,1-m],f(x)max<g(x)min
由(1)知,当m∈(-1,0)时,f(x)在[1,1-m]上单调递增,![]() ,
,
g(x)在[1,1-m]上单调递减,![]() ,
,
即证![]() ,化简得4(2-m)<e1-m[5-(1-m)]
,化简得4(2-m)<e1-m[5-(1-m)]
令1-m=t,t∈(1,2)
设h(t)=et(5-t)-4(t+1),t∈(1,2),
h′(t)=et(4-t)-4>2et-4>0,故h(t)在(1,2)上单调递增.
∴h(t)>h(1)=4e-8>0,即4(2-m)<e1-m[5-(1-m)]
故![]() ,得证.
,得证.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】已知一列非零向量![]() 满足:
满足:![]() ,
,![]() ,其中
,其中![]() 是正数
是正数
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:当![]() 时,向量
时,向量![]() 与
与![]() 的夹角为定值;
的夹角为定值;
(3)当![]() 时,把
时,把![]() 中所有与
中所有与![]() 共线的向量按原来的顺序排成一列,记为
共线的向量按原来的顺序排成一列,记为![]() ,令
,令![]() ,
,![]() 为坐标原点,求点列
为坐标原点,求点列![]() 的极限点
的极限点![]() 的坐标.(注:若点坐标为
的坐标.(注:若点坐标为![]() ,且
,且![]() ,则称点
,则称点![]() 为点列的极限点)
为点列的极限点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥P–ABC中,PA⊥平面ABC,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,则异面直线PC,AD所成角的余弦值为

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了110人,其中女性50人,男性60人.女性中有30人主要的休闲方式是看电视,另外20人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外40人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 列联表;
列联表;
(2)判断是否有99%的把握认为性别与休闲方式有关系.
下面临界值表供参考:
| 0.10 | 0.05 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
(参考公式: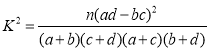 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家环境标准制定的空气质量指数与空气质量等级对应关系如表:
空气质量指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量等级 | 1级优 | 2级良 | 3级轻 度污染 | 4级中度污染 | 5级重 度污染 | 6级严重污染 |
由全国重点城市环境监测网获得10月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如图:

(1)试根据上面的统计数据,计算甲、乙两个城市的空气质量指数的方差;
(2)试根据上面的统计数据,估计甲城市某一天空气质量等级为2级良的概率;
(3)分别从甲城市和乙城市的统计数据中任取一个,试求两个城市空气质量等级相同的概率.供参考数据:292+532+572+752+1062=23760,432+412+552+582+782=16003
查看答案和解析>>
科目:高中数学 来源: 题型:
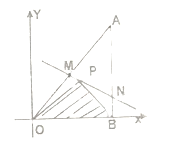
【题目】如图所示,将一块直角三角形木板![]() 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知![]() ,点
,点![]() 是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点
是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点![]() 的任一直线
的任一直线![]() 将三角形木板锯成
将三角形木板锯成![]() .设直线
.设直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求点![]() 的坐标及直线
的坐标及直线![]() 的斜率
的斜率![]() 的范围;
的范围;
(Ⅱ)令![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 的取值范围;
的取值范围;
(Ⅲ)令(Ⅱ)中![]() 的取值范围为集合
的取值范围为集合![]() ,若
,若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了诊断高三学生在市“一模”考试中文科数学备考的状况,随机抽取了50名学生的市“一模”数学成绩进行分析,将这些成绩分为九组,第一组[60,70),第二组[70,80),……,第九组[140,150],并绘制了如图所示的频率分布直方图.
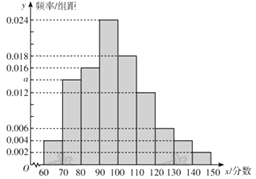
(1)试求出![]() 的值并估计该校文科数学成绩的众数和中位数;
的值并估计该校文科数学成绩的众数和中位数;
(2)现从成绩在[120,150]的同学中随机抽取2人进行谈话,那么抽取的2人中恰好有一人的成绩在[130,140)中的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,假命题的个数是( )
(1)若直线a在平面![]() 上,直线b不在平面
上,直线b不在平面![]() 上,则a,b是异面直线;
上,则a,b是异面直线;
(2)若a,b是异面直线、则与a,b都垂直的直线有且只有一条
(3)若a,b是异面直线、若c,d与直线a,b都相交,则c,d也是异面直线
(4)设a,b是两条直线,若![]() 平面
平面![]() ,
,![]() ,则
,则![]() 平面
平面![]() .
.
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com