
分析 (Ⅰ)求出导函数$f'(x)=\frac{1}{x}-a$,利用f(x) 在(0,+∞) 内必不单调,推出a>0,判断单调性,然后求解最值.
(Ⅱ)通过$\left\{\begin{array}{l}ln{x_1}-a{x_1}+b=0\\ ln{x_2}-a{x_2}+b=0\end{array}\right.$,两式相减得$ln\frac{x_1}{x_2}-a({x_1}-{x_2})=0$,得到$a=\frac{{ln\frac{x_1}{x_2}}}{{{x_1}-{x_2}}}$,故要证${x_1}{x_2}<\frac{1}{a^2}$,即证${ln^2}\frac{x_1}{x_2}<\frac{{{{({x_1}-{x_2})}^2}}}{{{x_1}{x_2}}}=\frac{x_1}{x_2}-2+\frac{x_2}{x_1}$,不妨设x1<x2,令$\frac{x_1}{x_2}=t∈(0,1)$,则只需证${ln^2}t<t-2+\frac{1}{t}$,构造函数$g(t)={ln^2}t-t-\frac{1}{t}+2$,通过函数的导数以及函数的单调性求解最值即可.
解答 (本小题满分12分)解:(Ⅰ)$f'(x)=\frac{1}{x}-a$,
∵f(x) 有两个不同的零点,∴f(x) 在(0,+∞) 内必不单调,故a>0,…1分
此时$f'(x)>0⇒x<\frac{1}{a}$,∴f(x)在$(0,\frac{1}{a})$上单增,$(\frac{1}{a},+∞)$上单减,…3分
∴$f{(x)_{max}}=f(\frac{1}{a})=-lna-1+b$,无最小值;…4分
(Ⅱ)由题知$\left\{\begin{array}{l}ln{x_1}-a{x_1}+b=0\\ ln{x_2}-a{x_2}+b=0\end{array}\right.$,两式相减得$ln\frac{x_1}{x_2}-a({x_1}-{x_2})=0$即$a=\frac{{ln\frac{x_1}{x_2}}}{{{x_1}-{x_2}}}$,…6分
故要证${x_1}{x_2}<\frac{1}{a^2}$,即证${x_1}{x_2}<\frac{{{{({x_1}-{x_2})}^2}}}{{{{ln}^2}\frac{x_1}{x_2}}}$,即证${ln^2}\frac{x_1}{x_2}<\frac{{{{({x_1}-{x_2})}^2}}}{{{x_1}{x_2}}}=\frac{x_1}{x_2}-2+\frac{x_2}{x_1}$,
不妨设x1<x2,令$\frac{x_1}{x_2}=t∈(0,1)$,则只需证${ln^2}t<t-2+\frac{1}{t}$,…9分
设$g(t)={ln^2}t-t-\frac{1}{t}+2$,则$g'(t)=2\frac{1}{t}lnt-1+\frac{1}{t^2}=\frac{{2lnt-t+\frac{1}{t}}}{t}$,
设$h(t)=2lnt-t+\frac{1}{t}$,则$h'(t)=-\frac{{{{(t-1)}^2}}}{t^2}<0$,∴h(t)在(0,1)上单减,∴h(t)>h(1)=0,
∴g(t)在(0,1)上单增,∴g(t)<g(1)=0,
即${ln^2}t<t-2+\frac{1}{t}$,在t∈(0,1)时恒成立,原不等式得证.…12分
点评 本题考查函数的导数的应用,函数的最值以及单调区间的求法,考查构造法的应用,转化思想以及计算能力.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-3,-\frac{5}{2})$ | B. | $(2,\frac{5}{2})$ | C. | $(\frac{5}{2},3)$ | D. | $(-3,\frac{5}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
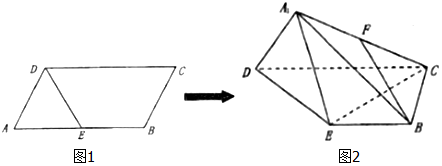
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥β,α⊥γ,则β⊥γ | B. | 若a,b与c所成的角相等,则a∥b | ||
| C. | 若α⊥α,α∥β,则α⊥β | D. | 若a∥b,a?α,则b∥α |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com