
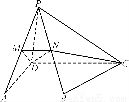
如图所示,四棱锥PABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=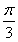 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.
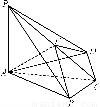
(1)求PA的长;
(2)求二面角B-AF-D的正弦值.
(1)2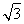 (2)
(2)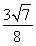
【解析】(1)如图,连结BD交AC于O,因为BC=CD,即△BCD为等腰三角形,又AC平分∠BCD,
故AC⊥BD.以O为坐标原点,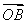 、
、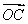 、
、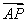 的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系Oxyz,则OC=CDcos
的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系Oxyz,则OC=CDcos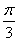 =1,而AC=4,得AO=AC-OC=3.又OD=CDsin
=1,而AC=4,得AO=AC-OC=3.又OD=CDsin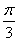 =
=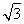 ,故A(0,-3,0),B(
,故A(0,-3,0),B(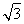 ,0,0),C(0,1,0),D(-
,0,0),C(0,1,0),D(-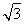 ,0,0).
,0,0).
因为PA⊥底面ABCD,可设P(0,-3,z),由F为PC边中点,得F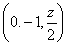 ,又
,又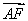 =
=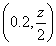 ,
,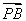 =(
=(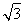 ,3,-z),因AF⊥PB,故
,3,-z),因AF⊥PB,故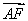 ·
·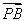 =0,即6-
=0,即6-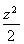 =0,z=2
=0,z=2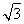 (舍去-2
(舍去-2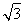 ),所以|
),所以|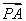 |=2
|=2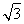 .
.
(2)由(1)知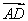 =(-
=(-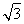 ,3,0),
,3,0),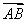 =(
=(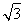 ,3,0),
,3,0),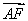 =(0,2,
=(0,2,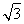 ).设平面FAD的法向量为n1=(x1,y1,z1),平面FAB的法向量为n2=(x2,y2,z2).
).设平面FAD的法向量为n1=(x1,y1,z1),平面FAB的法向量为n2=(x2,y2,z2).
由n1·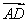 =0,n1·
=0,n1· =0,得
=0,得 因此可取n1=(3,
因此可取n1=(3,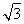 ,-2).
,-2).
由n2·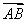 =0,n2·
=0,n2·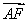 =0,得
=0,得 故可取n2=(3,-
故可取n2=(3,-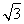 ,2).
,2).
从而向量n1,n2的夹角的余弦值为cos〈n1,n2〉=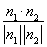 =
=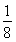 .
.
故二面角B-AF-D的正弦值为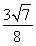 .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第4课时练习卷(解析版) 题型:解答题
某森林出现火灾,火势正以100m2/分钟的速度顺风蔓延,消防站接到报警立即派消防队员前去,在火灾发生后5分钟到达救火现场,已知消防队员在现场平均每人灭火50m2/分钟,所消耗的灭火材料,劳务津贴等费用为人均125元/分钟,另附加每次救火所耗损的车辆、器械和装备等费用人均100元,而烧毁森林的损失费60元/m2,应该派多少消防队员前去救火才能使总损失最少?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第2课时练习卷(解析版) 题型:填空题
设变量x、y满足约束条件: 则z=x-3y的最小值为________.
则z=x-3y的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第1课时练习卷(解析版) 题型:解答题
已知不等式(2+x)(3-x)≥0的解集为A,函数f(x)=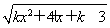 (k<0)的定义域为B.
(k<0)的定义域为B.
(1)求集合A;
(2)若集合B中仅有一个元素,试求实数k的值;
(3)若B?A,试求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:解答题
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
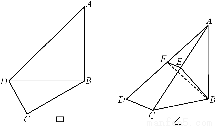
(1)求证:DC⊥平面ABC;
(2)求BF与平面ABC所成角的正弦值;
(3)求二面角B-EF-A的余弦值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:解答题
如图,圆锥的高PO=4,底面半径OB=2,D为PO的中点,E为母线PB的中点,F为底面圆周上一点,满足EF⊥DE.
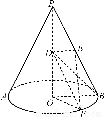
(1)求异面直线EF与BD所成角的余弦值;
(2)求二面角OOFE的正弦值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:填空题
已知l∥α,且l的方向向量为(2,m,1),平面α的法向量为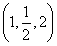 ,则m=________.
,则m=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:解答题
如图,在球面上有四个点P、A、B、C,如果PA、PB、PC两两互相垂直,且PA=PB=PC=a,求这个球的表面积.
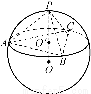
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:解答题
如图,在四棱锥PABCD中,PD⊥底面ABCD,AD⊥AB,CD∥AB,AB=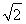 AD=2,CD=3,直线PA与底面ABCD所成角为60°,点M、N分别是PA、PB的中点.求证:
AD=2,CD=3,直线PA与底面ABCD所成角为60°,点M、N分别是PA、PB的中点.求证:
(1)MN∥平面PCD;
(2)四边形MNCD是直角梯形;
(3)DN⊥平面PCB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com