
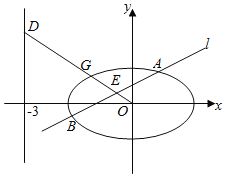
【题目】在平面直角坐标系xOy中,已知椭圆![]() ,如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于两点A,B,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=﹣3于点D(﹣3,m).
,如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于两点A,B,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=﹣3于点D(﹣3,m).
(1)求m2+k2的最小值;
(2)若|OG|2=|OD||OE|,求证:直线l过定点.
【答案】(1)2;(2)见解析
【解析】
(1)设出直线方程为![]() ,联立直线的方程和椭圆的方程,化简为一元二次方程的形式.根据直线和椭圆有两个交点得出判别式大于零,写出韦达定理,根据中点坐标公式求得
,联立直线的方程和椭圆的方程,化简为一元二次方程的形式.根据直线和椭圆有两个交点得出判别式大于零,写出韦达定理,根据中点坐标公式求得![]() 点的坐标,由此求得直线
点的坐标,由此求得直线![]() 的斜率和方程,根据
的斜率和方程,根据![]() 点坐标求得
点坐标求得![]() 的关系式,结合基本不等式求得
的关系式,结合基本不等式求得![]() 的最小值.(2)将直线
的最小值.(2)将直线![]() 的方程代入椭圆方程,求得
的方程代入椭圆方程,求得![]() 点坐标,结合
点坐标,结合![]() 两点坐标以及两点间的距离公式,求得
两点坐标以及两点间的距离公式,求得![]() ,代入
,代入![]() 列方程,解方程求得
列方程,解方程求得![]() 的关系,由此判断出直线过定点.
的关系,由此判断出直线过定点.
(1)设直线l的方程为y=kx+t(k>0),由题意,t>0,
由方程组 ,得(3k2+1)x2+6ktx+3t2﹣3=0,由题意△>0,所以3k2+1>t2,
,得(3k2+1)x2+6ktx+3t2﹣3=0,由题意△>0,所以3k2+1>t2,
设A(x1,y1),B(x2,y2),由根与系数的关系得![]() ,所以
,所以![]() ,
,
由于E为线段AB的中点,因此![]() ,
,
此时![]() ,所以OE所在直线的方程为
,所以OE所在直线的方程为![]() ,
,
又由题意知D(﹣3,m),令x=﹣3,得![]() ,即mk=1,
,即mk=1,
所以m2+k2≥2mk=2,当且仅当m=k=1时上式等号成立,
此时由△>0得0<t<2,因此当m=k=1且0<t<2时,m2+k2取最小值2.
(2)证明:由(1)知D所在直线的方程为![]() ,
,
将其代入椭圆C的方程,并由k>0,解得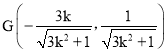 ,又
,又 ,
,
由距离公式及t>0得![]() ,
,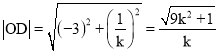 ,
,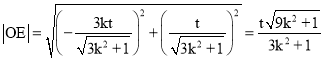 ,
,
由|OG|2=|OD||OE|,得t=k,
因此直线l的方程为y=k(x+1),所以直线l恒过定点(﹣1,0).


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】已知函数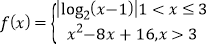 若方程f(x)=m有4个不同的实根x1,x2,x3,x4,且x1<x2<x3<x4,则(
若方程f(x)=m有4个不同的实根x1,x2,x3,x4,且x1<x2<x3<x4,则(![]() )(x3+x4)=( )
)(x3+x4)=( )
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,右焦点为
,右焦点为![]() ,且
,且![]() 上的动点
上的动点![]() 到
到![]() 的距离的最大值为4,最小值为2.
的距离的最大值为4,最小值为2.
(1)证明:![]() .
.
(2)若直线![]() :
:![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 均不与
均不与![]() ,
,![]() 重合),且
重合),且![]() ,试问
,试问![]() 是否经过定点?若经过,求出此定点坐标;若不经过,请说明理由.
是否经过定点?若经过,求出此定点坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个乒乓球协会分别选派3,1,2名运动员参加某次比赛,甲协会运动员编号分别为![]() ,
,![]() ,
,![]() ,乙协会编号为
,乙协会编号为![]() ,丙协会编号分别为
,丙协会编号分别为![]() ,
,![]() ,若从这6名运动员中随机抽取2名参加双打比赛.
,若从这6名运动员中随机抽取2名参加双打比赛.
(1)用所给编号列出所有可能抽取的结果;
(2)求丙协会至少有一名运动员参加双打比赛的概率;
(3)求参加双打比赛的两名运动员来自同一协会的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com