
【题目】选修![]() :不等式选讲
:不等式选讲
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
【答案】(1){x|-![]() };(2)m≤﹣
};(2)m≤﹣![]() 或m≥1.
或m≥1.
【解析】试题分析:
(Ⅰ)零点分段可得不等式的解集为{x|-![]() };
};
(Ⅱ)由题意得到关于实数m的不等式,求解不等式可得实数m的取值范围是m≤﹣![]() 或m≥1.
或m≥1.
试题解析:
(Ⅰ)不等式f(x)<8,即|2x+3|+|2x﹣1|<8,
可化为① 或②
或②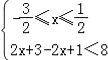 或③
或③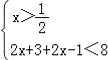 ,…
,…
解①得﹣![]() <x<﹣
<x<﹣![]() ,解②得﹣
,解②得﹣![]() ≤x≤
≤x≤![]() ,解③得
,解③得![]() <x<
<x<![]() ,
,
综合得原不等式的解集为{x|-![]() }.
}.
(Ⅱ)因为∵f(x)=|2x+3|+|2x﹣1|≥|(2x+3)﹣(2x﹣1)|=4,
当且仅当﹣![]() ≤x≤
≤x≤![]() 时,等号成立,即f(x)min=4,…
时,等号成立,即f(x)min=4,…
又不等式f(x)≤|3m+1|有解,则|3m+1|≥4,解得:m≤﹣![]() 或m≥1.
或m≥1.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,且
,且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .试比较
.试比较![]() 与0的关系,并给出理由.
与0的关系,并给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,离心率为
,离心率为![]() .设过点
.设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同两点
相交于不同两点![]() ,
, ![]() 周长为
周长为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点![]() ,证明:当直线
,证明:当直线![]() 变化时,总有TA与
变化时,总有TA与![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() +x在x=1处的切线方程为2x﹣y+b=0.
+x在x=1处的切线方程为2x﹣y+b=0.
(Ⅰ)求实数a,b的值;
(Ⅱ)若函数g(x)=f(x)+![]() x2﹣kx,且g(x)是其定义域上的增函数,求实数k的取值范围.
x2﹣kx,且g(x)是其定义域上的增函数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x∈A={x|x2﹣2x﹣3≤0,x∈R},q:x∈B={x|x2﹣2mx+m2﹣9≤0,x∈R,m∈R}.
(1)若A∩B=[1,3],求实数m的值;
(2)若p是q的充分条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合A是由且备下列性质的函数![]() 组成的:
组成的:
①函数![]() 的定义域是
的定义域是![]() ;②函数
;②函数![]() 的值域是
的值域是![]() ;
;
③函数![]() 在
在![]() 上是增函数,试分别探究下列两小题:
上是增函数,试分别探究下列两小题:
(1)判断函数数![]() 及
及![]() 是否属于集合A?并简要说明理由;
是否属于集合A?并简要说明理由;
(2)对于(1)中你认为属于集合A的函数![]() ,不等式
,不等式![]()
是否对于任意的![]() 恒成立?若成立,请给出证明;若不成立,请说明理由。
恒成立?若成立,请给出证明;若不成立,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两圆C1:x2+y2-2x-6y-1=0和C2:x2+y2-10x-12y+45=0.
(1)求证:圆C1和圆C2相交;
(2)求圆C1和圆C2的公共弦所在直线的方程和公共弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com