
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)设函数![]() ,
, ![]() .若函数
.若函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() ,
, ![]() 的定义域都是
的定义域都是![]() ,对于函数
,对于函数![]() 的图象上的任意一点
的图象上的任意一点![]() ,在函数
,在函数![]() 的图象上都存在一点
的图象上都存在一点![]() ,使得
,使得![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数, ![]() 为坐标原点.求
为坐标原点.求![]() 的取值范围.
的取值范围.
【答案】(1)(2)
【解析】试题分析:求函数的单调区间可利用求导完成,求函数的最值可通过求导研究函数的单调性求出极值,并与区间端点函数值比较得出最值;解决![]() 问题,先求出
问题,先求出![]() 斜率的取值范围,根据垂直关系得出
斜率的取值范围,根据垂直关系得出![]() 斜率的取值范围,转化为恒成立问题,借助恒成立思想解题.
斜率的取值范围,转化为恒成立问题,借助恒成立思想解题.
试题解析:
(1)当![]() 时,
时, ![]() ,
, ![]() .
.
因为![]() 在
在![]() 上单调增,且
上单调增,且![]() ,
,
所以当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以函数![]() 的单调增区间是
的单调增区间是![]() .
.
(2)![]() ,则
,则![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在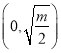 上单调减;
上单调减;
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在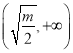 上单调增.
上单调增.
所以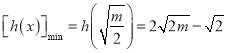 .
.
①当![]() ,即
,即![]() 时,
时,
函数![]() 的最小值
的最小值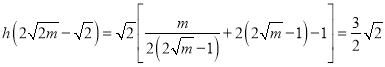 ,
,
即![]() ,解得
,解得![]() 或
或![]() (舍),所以
(舍),所以![]() ;
;
②当![]() ,即
,即![]() 时,
时,
函数![]() 的最小值
的最小值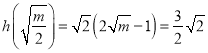 ,解得
,解得![]() (舍).
(舍).
综上所述, ![]() 的值为
的值为![]() .
.
(3)由题意知, ![]() ,
, ![]() .
.
考虑函数![]() ,因为
,因为![]() 在
在![]() 上恒成立,
上恒成立,
所以函数![]() 在
在![]() 上单调增,故
上单调增,故![]() .
.
所以![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立.
上恒成立.
设![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上单调减,所以
上单调减,所以![]() .
.
设![]() ,
,
则![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上单调增,所以
上单调增,所以![]() .
.
综上所述, ![]() 的取值范围为
的取值范围为![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
车间 | A | B | C |
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品来自相同车间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图△ABC是等腰三角形,BA=BC,DC⊥平面ABC,AE∥DC,若AC=2且BE⊥AD,则( ) 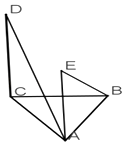
A.AB+BC有最大值
B.AB+BC有最小值
C.AE+DC有最大值
D.AE+DC有最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 与动直线
与动直线![]() 的交点为
的交点为![]() ,线段
,线段![]() 的中垂线与动直线
的中垂线与动直线![]() 的交点为
的交点为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过动点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() ,求证:
,求证: ![]() 的大小为定值.
的大小为定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为ɑ 的正方体ABCD﹣A1B1C1D1中,E、F、G分别是CB.CD.CC1的中点. 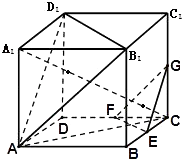
(1)求直线 A1C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F为CE上的点,且BF⊥平面ACE,AC,BD交于G点 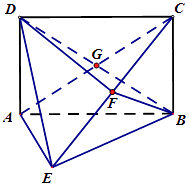
(1)求证:AE∥平面BFD
(2)求证:AE⊥平面BCE
(3)求三棱柱C﹣BGF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,已知PA⊥平面ABCD,AD∥BC,AD⊥AB,PA=AD=2BC=2AB=2. 
(1)求证:平面PAC⊥平面PCD;
(2)若E是PD的中点,求平面BCE将四棱锥P﹣ABCD分成的上下两部分体积V1、V2之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com