
分析 根据所给的示例及类比推理的规则得出高维的测度的导数是底一维的测度,从而得到W′=V,从而求出所求.
解答 解:∵二维空间中圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2,观察发现S′=l
三维空间中球的二维测度(表面积)S=4πr2,三维测度(体积)V=$\frac{4}{3}$πr3,观察发现V′=S
∴四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W,则W′=V=8πr3;
∴W=2πr4.
故答案为:2πr4
点评 本题考查类比推理,解题的关键是理解类比的规律,解题的关键主要是通过所给的示例及类比推理的规则得出高维的测度的导数是低一维的测度,属于基础题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (±$\sqrt{7}$,0) | B. | (0,±$\sqrt{7}$) | C. | (±5,0) | D. | (0,±5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
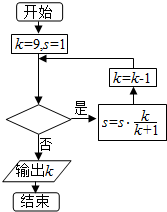
| A. | s>$\frac{1}{2}$ | B. | s>$\frac{3}{5}$ | C. | s>$\frac{7}{10}$ | D. | s>$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
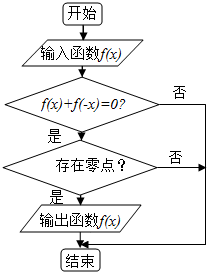 某程序框图如图所示,现输入如下四个函数,其中可以输出的函数是f(x)=sinx.
某程序框图如图所示,现输入如下四个函数,其中可以输出的函数是f(x)=sinx.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
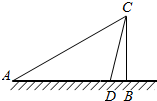 如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )
如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )| A. | 50($\sqrt{3}$+1)m | B. | 50($\sqrt{2}$+1)m | C. | 50($\sqrt{3}$-1)m | D. | 50($\sqrt{3}$+$\sqrt{2}$) m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com