
 }满足
}满足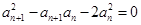 (
(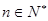 ),且
),且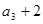 是
是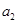 ,
,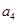 的等差中项.
的等差中项.  }的通项公式
}的通项公式 ;
;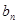 =
=
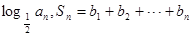 ,是否存在正整数
,是否存在正整数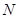 ,使
,使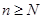 时,不等式
时,不等式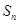
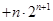
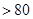 恒成立,若存在,求
恒成立,若存在,求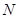 的值;不存在,说明理由.
的值;不存在,说明理由. . (Ⅱ)
. (Ⅱ) .
. 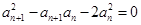 ,得
,得 。
。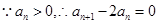 。数列{
。数列{ }是以2为公比的等比数列.根据题意可求得
}是以2为公比的等比数列.根据题意可求得 ,
, (2)由(Ⅰ)及
(2)由(Ⅰ)及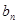 =
=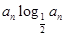 得,
得, 。利用错位相减法求出
。利用错位相减法求出 。要使
。要使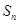
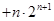
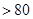 成立,只需
成立,只需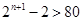 成立,即
成立,即 ,
,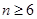 ,取
,取 。
。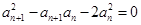 ,
, ,....................................2分
,....................................2分 }的各项均为正数,∴
}的各项均为正数,∴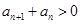 ,
, ,
,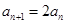 (
(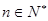 ),所以数列{
),所以数列{ }是以2为公比的等比数列.…………3分
}是以2为公比的等比数列.…………3分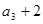 是
是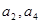 的等差中项,
的等差中项,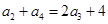 ,∴
,∴ ,∴
,∴ ,
, }的通项公式
}的通项公式 .……………………………………………………6分
.……………………………………………………6分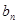 =
=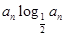 得,
得, , ……………………………8分
, ……………………………8分 ,
,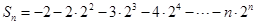 1
1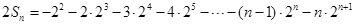 ②
②
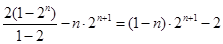 ……………………………10分
……………………………10分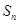
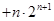
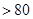 成立,只需
成立,只需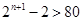 成立,即
成立,即 ,
,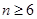 ,
, 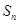
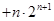
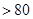 成立,取
成立,取 . …………13分
. …………13分

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com