
分析 (1)利用赋值法即可求f(0),根据函数f(x)的奇偶性的定义,即可得到结论;
(2)根据函数单调性的定义即可判断f(x)的单调性;
(3)将不等式进行等价转化,结合函数的奇偶性和单调性的性质即可得到结论.
解答 解:(1)f(x)是奇函数.
∵f(x)对一切x,y∈R都有f(x+y)=f(x)+f(y),
令x=y=0,得:f(0)=f(0)+f(0),∴f(0)=0,
令y=-x,得f(x-x)=f(x)+f(-x)=f(0)=0,
∴f(-x)=-f(x),∴f(x)是奇函数.
(2)f(x)在R上是减函数.
∵f(x)对一切x,y∈R都有f(x+y)=f(x)+f(y),
当x>0时,恒有f(x)<0.
令x1>x2,则x1-x2>0,且f(x1-x2)=f(x1)+f(-x2)<0,
由(1)知,f(x2)-f(x1)<0,∴f(x2)<f(x1).
∴f(x)在R上是减函数.
(3)∵f(2)=1,
∴2f(x)=f(x)+f(x)=f(2x),
f(2)+f(2)=f(4)=1+1=2,
f(4)+f(4)=f(8)=2+2=4,
即不等式f(-x2)+2f(x)+4≤0等价为不等式f(-x2)+f(2x)+f(8)≤0,
即f(-x2+2x)+f(8)≤0,
即f(-x2+2x)≤-f(8)=f(-8),
∵f(x)在R上是减函数,
∴-x2+2x≥-8,
即x2-2x-8≤0,
即-2≤x≤4,
即不等式的解集为[-2,4].
点评 本题主要考查抽象函数的应用,利用赋值法结合函数单调性和奇偶性的定义是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | 8 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
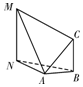 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从M点测得A点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°;已知山高BC=200m,则山高MN=( )
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从M点测得A点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°;已知山高BC=200m,则山高MN=( )| A. | 300m | B. | 200$\sqrt{2}$m | C. | 200$\sqrt{3}$m | D. | 300$\sqrt{2}$m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
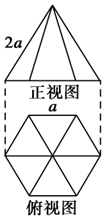 如图是一个几何体的正视图和俯视图.
如图是一个几何体的正视图和俯视图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com