
【题目】已知椭圆![]() :
:![]() 的短轴长为2,离心率
的短轴长为2,离心率![]() .过椭圆的右焦点作直线l(不与
.过椭圆的右焦点作直线l(不与![]() 轴重合)与椭圆
轴重合)与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)试问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 恰好关于
恰好关于![]() 轴对称?若存在,求出点
轴对称?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】某工厂A,B两条生产线生产同款产品,若该产品按照一、二、三等级分类,则每件可分别获利10元、8元、6元,现从A,B生产线的产品中各随机抽取100件进行检测,结果统计如下图:
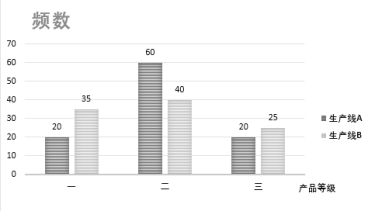
(I)根据已知数据,判断是否有![]() 的把握认为一等级产品与生产线有关?
的把握认为一等级产品与生产线有关?
(II)求抽取的200件产品的平均利润;
(III)估计该厂若产量为2000件产品时,一等级产品的利润.
附:独立性检验临界值表
|
|
|
|
|
|
|
|
|
|
| … |
|
|
|
|
|
|
|
|
|
|
| … |
(参考公式: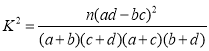 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
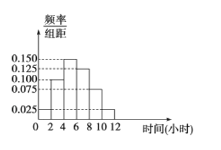
【题目】某中学共有1000人,其中男生700人,女生300人,为了了解该校学生每周平均体育锻炼时间的情况以及经常进行体育锻炼的学生是否与性别有关(经常进行体育锻炼是指:周平均体育锻炼时间不少于4小时),现在用分层抽样的方法从中收集200位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如图.已知在样本数据中,有40位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理( )
附: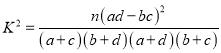 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A.有95%的把握认为“该校学生每周平均体育锻炼时间与性别无关”
B.有90%的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C.有90%的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D.有95%的把握认为“该校学生每周平均体育锻炼时间与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省从2021年开始,高考采用取消文理分科,实行“![]() ”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的
”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的![]() 列联表.
列联表.
性别 | 选择物理 | 选择历史 | 总计 |
男生 | ________ | 50 |
|
女生 | 30 | ________ |
|
总计 | ________ | ________ | 200 |
(1)求![]() ,
,![]() 的值;
的值;
(2)请你依据该列联表判断是否有99.5%的把握认为选择科目与性别有关?说明你的理由.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001/span> |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为原点,过原点的直线(不与
为原点,过原点的直线(不与![]() 轴垂直)与椭圆
轴垂直)与椭圆![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 、
、![]() 与
与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .问:
.问:![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉市掀起了轰轰烈烈的“十日大会战”,要在10天之内,对武汉市民做一次全员检测,彻底摸清武汉市的详细情况.某医院为筛查冠状病毒,需要检验血液是否为阳性,现有![]() 份血液样本,有以下两种检验方式:
份血液样本,有以下两种检验方式:
方案①:将每个人的血分别化验,这时需要验1000次.
方案②:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血就只需检验一次(这时认为每个人的血化验
个人的血就只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验这样,该组
个人的血样再分别进行一次化验这样,该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次. 假设此次检验中每个人的血样化验呈阳性的概率为
次. 假设此次检验中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案②中,某组![]() 个人中每个人的血化验次数为
个人中每个人的血化验次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)设![]() . 试比较方案②中,
. 试比较方案②中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以减少多少次?(最后结果四舍五入保留整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(在花卉进行硬枝扦插过程中,常需要用生根粉调节植物根系生长.现有20株使用了生根粉的花卉,在对最终“花卉存活”和“花卉死亡”进行统计的同时,也对在使用生根粉2个小时后的生根量进行了统计,这20株花卉生根量如下表所示,其中生根量在6根以下的视为“不足量”,大于等于6根为“足量”.现对该20株花卉样本进行统计,其中“花卉存活”的13株.已知“花卉存活”但生根量“不足量”的植株共1株.
编号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
生根量 | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 9 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
(1)完成![]() 列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“花卉的存活”与“生根足量”有关?
列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“花卉的存活”与“生根足量”有关?
生根足量 | 生根不足量 | 总计 | |
花卉存活 | |||
花卉死亡 | |||
总计 | 20 |
(2)若在该样本“生根不足量”的植株中随机抽取3株,求这3株中恰有1株“花卉存活”的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
独立性检验中的 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com