【题目】已知某运动员每次投篮命中的概率低于
，现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器产生0到9之间取整数值的随机数，指定1，2，3，4表示命中，5，6，7，8，9，0表示不命中；再以每三个随机数为一组，代表三次投篮的结果.经随机模拟产生了如下20组随机数：
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计，该运动员三次投篮恰有两次命中的概率为（ ）
A.0.35B.0.25C.0.20D.0.15
科目：高中数学 来源： 题型：
【题目】参加衡水中学数学选修课的同学，对某公司的一种产品销量与价格进行统计，得到如下数据和散点图：
定价 |
|
|
|
|
|
|
年销售 |
|
|
|
|
|
|
|
|
|
|
|
|
|
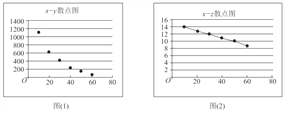
（参考数据：
）
（I）根据散点图判断，
与
，
与哪一对具有较强的线性相关性（给出判断即可，不必说明理由）？
（II）根据（I）的判断结果有数据，建立关于的回归方程（方程中的系数均保留两位有效数字）；
（III）定价为多少元/
时，年利润的预报值最大？
附：对一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为：
.
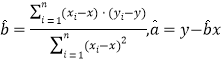查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地区不同身高
的未成年男性的体重平均值
如下表：
身高x（cm） | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 |
体重y(kg) | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 | 20.92 | 26.86 | 31.11 |
已知
与
之间存在很强的线性相关性，
（Ⅰ）据此建立
与之间的回归方程；
（Ⅱ）若体重超过相同身高男性体重平均值的
倍为偏胖，低于
倍为偏瘦，那么这个地区一名身高
体重为
的在校男生的体重是否正常？
参考数据：
附：对于一组数据
，其回归直线
中的斜率和截距的最小二乘估计分别为
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，其图象相邻两条对称轴之间的距离为
，将该函数的图象向左平移
个单位后，得到的图象对应的函数为偶函数．下列判断正确的是（ ）
A. 函数
的最小正周期为
B. 函数的图象关于点
对称
C. 函数的图象关于直线
对称
D. 函数在
上单调递增
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2018年，某地认真贯彻落实中央十九大精神和各项宏观调控政策，经济运行平稳增长，民生保障持续加强，惠民富民成效显著，城镇居民收入稳步增长，收入结构稳中趋优.据当地统计局公布的数据，现将8月份至12月份当地的人均月收入增长率与人均月收入分别绘制成折线图（如图一）与不完整的条形统计图（如图二）.请从图中提取相关的信息：
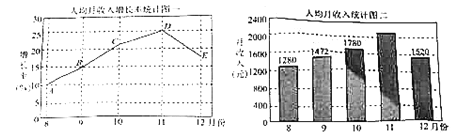
①10月份人均月收入增长率为
左右；
②11月份人均月收入为2047元；
③从上图可知该地9月份至12月份人均月收入比8月份人均月收入均得到提高.
其中正确的信息个数为（ ）
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设{an}是公比为 q的等比数列，且a1，a3，a2成等差数列．
（Ⅰ）求q的值；
（Ⅱ）设{bn}是以2为首项，q为公差的等差数列，其前n项和为Sn，当n≥2时，比较Sn与bn的大小，并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
