
【题目】已知定义域为R的函数 ![]() 是奇函数.
是奇函数.
(1)求a值;
(2)判断并证明该函数在定义域R上的单调性;
(3)设关于x的函数F(x)=f(4x﹣b)+f(﹣2x+1)有零点,求实数b的取值范围.
【答案】
(1)解:∵f(x)的定义域为R且为奇函数,
∴f(0)= ![]() =0,解得a=1,经检验符合.
=0,解得a=1,经检验符合.
(2)解:∵ ![]() ,f(x)在R上位减函数
,f(x)在R上位减函数
证明:设x1<x2,
则 ![]()
![]() ,(∵
,(∵ ![]() )
)
∴f(x)在R上是减函数.
(3)解:由F(x)=0,
得f(4x﹣b)+f(﹣2x+1)=0,
∵函数f(x)是奇函数
∴f(4x﹣b)=f(2x+1)
即4x﹣b=2x+1有解,
∴b=4x﹣2x+1=(2x)2﹣22x≥﹣1,
∴实数b的取值范围是b≥﹣1
【解析】(1)利用函数是奇函数,由f(0)=0,即可求a值;(2)利用函数单调性定义判断并证明该函数在定义域R上的单调性;(3)利用函数的奇偶性和函数零点的定义,求b的取值范围.
【考点精析】利用函数单调性的判断方法和函数的奇偶性对题目进行判断即可得到答案,需要熟知单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;偶函数的图象关于y轴对称;奇函数的图象关于原点对称.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣a)(x﹣b)(其中a>b),若f(x)的图象如图所示,则函数g(x)=ax+b的图象大致为( ) 
A.
B.
C.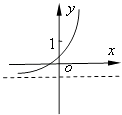
D.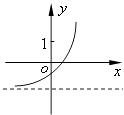
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c(a≠0)的图象过点(0,1)且与x轴有唯一的交点(﹣1,0).
(1)求f(x)的表达式;
(2)在(1)的条件下,设函数F(x)=f(x)﹣mx,若F(x)在区间[﹣2,2]上是单调函数,求实数m的取值范围;
(3)设函数g(x)=f(x)﹣kx,x∈[﹣2,2],记此函数的最小值为h(k),求h(k)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台举行一个比赛类型的娱乐节目, ![]() 两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将
两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将![]() 队第六位选手的成绩没有给出,并且告知大家
队第六位选手的成绩没有给出,并且告知大家![]() 队的平均分比
队的平均分比![]() 队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.

(1)根据茎叶图中的数据,求出![]() 队第六位选手的成绩;
队第六位选手的成绩;
(2)主持人从![]() 队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
(3)主持人从![]() 两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为
两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(x+1)﹣f(x)=2x(x∈R),且f(0)=1,
(1)求f(x)的解析式;
(2)当x∈[﹣1,1]时,求函数g(x)=f(x)﹣2x的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种机器的固定成本为0.5万元,但每生产1百台时,又需可变成本(即另增加投入)0.25万元.市场对此商品的年需求量为5百台,销售的收入(单位:万元)函数为:R(x)=5x﹣ ![]() x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
(1)将利润表示为产量的函数;
(2)年产量是多少时,企业所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是双曲线E:
分别是双曲线E: ![]()
![]() 的左、右焦点,P是双曲线上一点,
的左、右焦点,P是双曲线上一点, ![]() 到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当
到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当![]() 时,
时, ![]() 的面积为
的面积为![]() ,求此双曲线的方程。
,求此双曲线的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,上焦点
,上焦点![]() 到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=
到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=![]() .
.
(I)求椭圆C的标准方程;
(II)设过椭圆C的上顶点A的直线![]() 与椭圆交于点B(B不在y轴上),垂直于
与椭圆交于点B(B不在y轴上),垂直于![]() 的直线与
的直线与![]() 交于点M,与
交于点M,与![]() 轴交于点H,若
轴交于点H,若![]() =0,且
=0,且![]() ,求直线
,求直线![]() 的方程.
的方程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com