解:(1)由

•

=cosA-

sinA=-1,得到cosA=

sinA-1,代入sin
2A+cos
2A=1中得:
sin
2A+
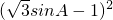
=1,化简得:sinA(2sinA-

)=0,因为sinA≠0,所以2sinA-

=0即sinA=

因为A∈(0,180°),所以A=60°或120°;
(2)由

•

=|

|•|

|cosA=bccosA=2,因为cosA=

(cosA=-

舍去),则bc=4①,
而a
2=b
2+c
2-2bccosA=b
2+c
2-4=4,所以b
2+c
2=8②,联立①②,解得b=2,c=2.
分析:(1)利用平面向量数量积的运算法则化简

•

=-1,得到关于cosA和sinA的关系式,利用同角三角函数间的平方关系化简可得sinA的值,根据A的范围及特殊角的三角函数值即可求出A的度数;
(2)利用平面向量数量积的运算法则化简

•

=2,得到bc=4记作①,然后利用余弦定理表示出a
2的关系式,把a的值代入即可得到b
2+c
2=8记作②,联立①②即可求出b和c的值.
点评:此题考查学生灵活运用平面向量数量积的运算法则化简求值,利用运用同角三角函数间的基本关系及余弦定理化简求值,是一道综合题.学生做题时应注意角度的范围,以及理解cosA=-

舍去的原因是bc>0.

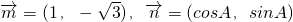 ,且
,且 .
.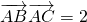 ,求b,c.
,求b,c. •
• =cosA-
=cosA- sinA=-1,得到cosA=
sinA=-1,得到cosA= sinA-1,代入sin2A+cos2A=1中得:
sinA-1,代入sin2A+cos2A=1中得: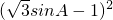 =1,化简得:sinA(2sinA-
=1,化简得:sinA(2sinA- )=0,因为sinA≠0,所以2sinA-
)=0,因为sinA≠0,所以2sinA- =0即sinA=
=0即sinA=
 •
• =|
=| |•|
|•| |cosA=bccosA=2,因为cosA=
|cosA=bccosA=2,因为cosA= (cosA=-
(cosA=- 舍去),则bc=4①,
舍去),则bc=4①, •
• =-1,得到关于cosA和sinA的关系式,利用同角三角函数间的平方关系化简可得sinA的值,根据A的范围及特殊角的三角函数值即可求出A的度数;
=-1,得到关于cosA和sinA的关系式,利用同角三角函数间的平方关系化简可得sinA的值,根据A的范围及特殊角的三角函数值即可求出A的度数; •
• =2,得到bc=4记作①,然后利用余弦定理表示出a2的关系式,把a的值代入即可得到b2+c2=8记作②,联立①②即可求出b和c的值.
=2,得到bc=4记作①,然后利用余弦定理表示出a2的关系式,把a的值代入即可得到b2+c2=8记作②,联立①②即可求出b和c的值. 舍去的原因是bc>0.
舍去的原因是bc>0. 

 名校课堂系列答案
名校课堂系列答案 β,则a∥b; ④若a与b异面,且a∥β,则b与β相交;
β,则a∥b; ④若a与b异面,且a∥β,则b与β相交;