[题目]已知为双曲线:的一个焦点.过作的一条渐近线的垂线.垂足为点.与的另一条渐近线交于点.若.则的离心率为( )A.2B.C.D. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知为双曲线：的一个焦点，过作的一条渐近线的垂线，垂足为点，与的另一条渐近线交于点，若，则的离心率为（）

A.2B.C.D.

【答案】C

【解析】

根据列方程，求得，由此求得，进而求得椭圆的离心率.

依题意，双曲线的渐近线方程为或.不妨设过作的一条渐近线的垂线，垂足为点，与的另一条渐近线交于点，如下图所示.

点到渐近线即的距离为.所以.由于，

所以.设，则，

即，即，解得（负根舍去），

即，所以.故C选项正确.

依题意，双曲线的渐近线方程为或.不妨设过作的一条渐近线的垂线，垂足为点，与的另一条渐近线交于点，如下图所示.

点到渐近线即的距离为.所以.

由于，所以.所以.

根据双曲线渐近线的对称性可知：，所以，

此时，即不符合题意.

故选：C

练习册系列答案

小学生10分钟口算测试100分系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系中，曲线的参数方程为（为参数）．以坐标原点为极点，轴的正半轴为极轴，建立极坐标系，直线的极坐标方程为．

（Ⅰ）求曲线的普通方程与直线的直角坐标方程；

（Ⅱ）若与平行的直线与曲线交于，两点．且在轴的截距为整数，的面积为，求直线的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】2021年起，我省将实行“3+1+2”高考模式，某中学为了解本校学生的选考情况，随机调查了100位学生，其中选考化学或生物的学生共有70位，选考化学的学生共有40位，选考化学且选考生物的学生共有20位．若该校共有1500位学生，则该校选考生物的学生人数的估计值为（）

A.300B.450C.600D.750

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为了更好地支持“中小型企业”的发展，某市决定对部分企业的税收进行适当的减免，某机构调查了当地的中小型企业年收入情况，并根据所得数据画出了样本的频率分布直方图，下面三个结论：

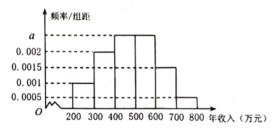
①样本数据落在区间的频率为0.45；

②如果规定年收入在500万元以内的企业才能享受减免税政策，估计有55%的当地中小型企业能享受到减免税政策；

③样本的中位数为480万元.

其中正确结论的个数为（）

A.0B.1C.2D.3

查看答案和解析>>

科目：高中数学 来源： 题型：

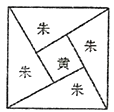
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明，下面是赵爽的弦图及注文，弦图是一个以勾股形之弦为边的正方形，其面积称为弦实，图中包含四个全等的勾股形及一个小正方形，分别涂成红（朱）色及黄色其面积称为朱实，黄实，利朱用2×勾×股+（股-勾）2=4×朱实+黄实=弦实，化简得勾2+股2=弦2，设勾股中勾股比为，若向弦图内随机抛掷1000颗图钉（大小忽略不计），则落在黄色图形内的图钉数大约为( )

A.886B.500C.300D.134

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】《普通高中数学课程标准（2017版）》提出了数学学科的六大核心素养.为了比较甲、乙两名高二学生的数学核心素养水平，现以六大素养为指标对二人进行了测验，根据测验结果绘制了雷达图（如图，每项指标值满分为5分，分值高者为优），则下面叙述正确的是（）

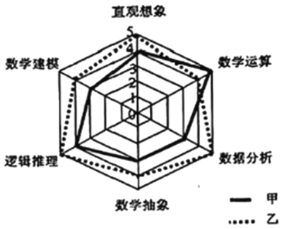
A.甲的数据分析素养高于乙

B.甲的数学建模素养优于数学抽象素养

C.乙的六大素养中逻辑推理最差

D.乙的六大素养整体平均水平优于甲

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知，是椭圆T.上的两点，且A点位于第一象限.过A做x轴的垂线，垂足为点C，点D满足，延长交T于点.

（1）设直线，的斜率分别为，.

（i）求证：；

（ii）证明：是直角三角形；

（2）求的面积的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某中学有初中学生1800人，高中学生1200人，为了解学生本学期课外阅读时间，现采用分成抽样的方法，从中抽取了100名学生，先统计了他们课外阅读时间，然后按“初中学生”和“高中学生”分为两组，再将每组学生的阅读时间（单位：小时）分为5组：[0，10），[10，20），[20，30），[30，40），[40，50]，并分别加以统计，得到如图所示的频率分布直方图．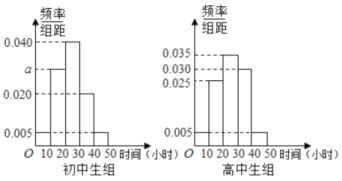

（1）写出的值；试估计该校所有学生中，阅读时间不小于30个小时的学生人数；
（2）从阅读时间不足10个小时的样本学生中随机抽取3人，并用表示其中初中生的人数，求的分布列和数学期望．