
分析 可令y=1,f(x)=f(x+1)+f(x-1),两次将x换为x+1,可得f(x)的周期为3,由题意可得方程的根的个数.
解答 解:2f(x)•f(y)=f(x+y)+f(x-y),f(1)=$\frac{1}{2}$,
令y=1,可得2f(x)f(1)=f(x+1)+f(x-1),
即为f(x)=f(x+1)+f(x-1),
将x换为x+1,可得f(x+1)=f(x+2)+f(x),
即有f(x+2)=f(x-1),
将x换为x+1,可得f(x+3)=f(x),
则函数f(x)以3为最小正周期的函数,
由f(1)=$\frac{1}{2}$,且f(x)在[0,3]上单调递减,
可得方程f(x)=$\frac{1}{2}$在[0,2014]之间有672个根,
在[-2014,0]之间有671个根,
则方程f(x)=$\frac{1}{2}$在区间[-2014,2014]内根的个数为672+671=1343个根.
故答案为:1343.
点评 本题考查抽象函数的性质和运用,主要是周期性的应用,考查运算能力,属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
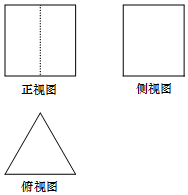 某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )
某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是( )| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $\frac{2}{3}\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
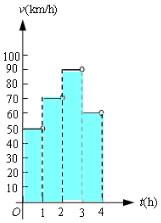 一辆汽车在某段路程中的行驶速率与时间的关系如图所示.
一辆汽车在某段路程中的行驶速率与时间的关系如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,直线l是曲线y=f(x)在x=3处的切线,f'(x)表示函数f(x)的导函数,则f(3)+f'(3)的值为$\frac{7}{3}$.
如图,直线l是曲线y=f(x)在x=3处的切线,f'(x)表示函数f(x)的导函数,则f(3)+f'(3)的值为$\frac{7}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{14}$ | B. | $\sqrt{13}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com