
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() .
.
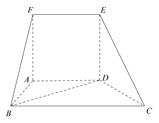
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】在实数集![]() 中,定义两个实数
中,定义两个实数![]() 、
、![]() 的运算法则△如下:若
的运算法则△如下:若![]() ,则
,则![]() ,若
,若![]() ,则
,则![]() .
.
(1)请分别计算![]() 和
和![]() 的值;
的值;
(2)对于实数![]() ,判断
,判断![]() 是否恒成立,并说明理由;
是否恒成立,并说明理由;
(3)求函数![]() 的解析式,其中
的解析式,其中![]() ,并求函数的最值.(符号“
,并求函数的最值.(符号“![]() ”表示相乘)
”表示相乘)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①存在实数x,使得sin x+cos x=2;
②函数y=cos![]() 是奇函数;
是奇函数;
③若角α,β是第一象限角,且α<β,则tan α<tan β;
④函数y=sin![]() 的图象关于点(
的图象关于点(![]() ,0)成中心对称.
,0)成中心对称.
⑤直线x=![]() 是函数y=sin
是函数y=sin![]() 图象的一条对称轴;
图象的一条对称轴;
其中正确的命题是( ).
A.②④B.①③C.①④D.②⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】旅行社为某旅行团包飞机去旅游,其中旅行社的包机费为15000元.旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数不超过35人时,飞机票每张收费800元;若旅游团的人数多于35人,则给予优惠,每多1人,机票费每张减少10元,但旅游团的人数最多有60人.设旅行团的人数为![]() 人,飞机票价格为
人,飞机票价格为![]() 元,旅行社的利润为
元,旅行社的利润为![]() 元.
元.
(1)写出飞机票价格![]() 元与旅行团人数
元与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)当旅游团的人数![]() 为多少时,旅行社可获得最大利润?求出最大利润.
为多少时,旅行社可获得最大利润?求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为![]() (
(![]() )件.当
)件.当![]() 时,年销售总收人为(
时,年销售总收人为(![]() )万元;当
)万元;当![]() 时,年销售总收人为
时,年销售总收人为![]() 万元.记该工厂生产并销售这种产品所得的年利润为
万元.记该工厂生产并销售这种产品所得的年利润为![]() 万元.(年利润=年销售总收入一年总投资)
万元.(年利润=年销售总收入一年总投资)
(1)求![]() (万元)与
(万元)与![]() (件)的函数关系式;
(件)的函数关系式;
(2)当该工厂的年产量为多少件时,所得年利润最大?最大年利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知acosC+ccosA=2bcosA.
(1)求角A的值;
(2)求sinB+sinC的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让学生更多的了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,统计结果见下表.请你根据频率分布表解答下列问题:
序号 | 分组(分数) | 组中值 | 频数(人数) | 频率 |
1 |
| 65 | ① | 0.12 |
2 |
| 75 | 20 | ② |
3 |
| 85 | ③ | 0.24 |
4 |
| 95 | ④ | ⑤ |
合计 | 50 | 1 |
(1)填充频率分布表中的空格;
(2)规定成绩不低于85分的同学能获奖,请估计在参加的800名学生中大概有多少名同学获奖?
(3)在上述统计数据的分析中有一项计算见算法流程图,求输出的![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com