
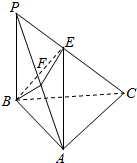
 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=4,点E、F分别为PC、PA的中点.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=4,点E、F分别为PC、PA的中点.分析 (几何法)(1)证明:PB⊥AC,$BE⊥AC\\ 由PB=BC.E是PC的中点,得BE⊥PC\\ 而AC∩PC=C$,然后证明$BE⊥平面PAC\end{array}$
(2)利用VF-ABE=VE-ABF=$\frac{1}{2}$VE-ABP=$\frac{1}{4}{V}_{C-ABP}$=$\frac{1}{4}{V}_{P-ABC}$,转化求解即可.
(向量法)以点C为原点建立空间直角坐标系C-XYZ(其中Z轴∥PB),(1)通过数量积证明BE⊥CA,结合BE⊥CP,证明BE⊥平面PAC,
(2)利用VF-ABE=VE-ABF,求得平面ABF的一个法向量,然后求出E到平面ABF的距离,然后求解体积.
解答  (几何法)(1)证明:∵PB⊥底面ABC,AC?平面ABC,
(几何法)(1)证明:∵PB⊥底面ABC,AC?平面ABC,
∴PB⊥AC,又∠BCA=90°,即AC⊥BC,而PB∩BC=B,∴AC⊥平面PBC,
又BE?平面PBC,∴$BE⊥AC\\ 由PB=BC.E是PC的中点,得BE⊥PC\\ 而AC∩PC=C$,∴$BE⊥平面PAC\end{array}$
(2)解:VF-ABE=VE-ABF=$\frac{1}{2}$=
VE-ABP=$\frac{1}{4}{V}_{C-ABP}$=$\frac{1}{4}{V}_{P-ABC}$=$\frac{1}{4}×\frac{1}{3}{S}_{△ABC}•PB$=$\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×4×4×4$=$\frac{8}{3}$.
(向量法)如图,以点C为原点建立空间直角坐标系C-XYZ(其中Z轴∥PB),
由已知,得: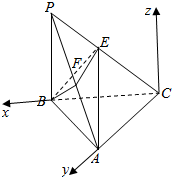
C(0,0,0),A(0,4,0),B(4,0,0),P(4,0,4),E(2,0,2),F(2,2,2)
(1)证明:$\overrightarrow{BE}=({-2,0,2}),\overrightarrow{CA}=({0,4,0}),\overrightarrow{CP}=({4,0,4})$,
$\begin{array}{c}∴\overrightarrow{BE}•\overrightarrow{CA}=-2×0+0×4+2×0=0\end{array}\right.$$\overrightarrow{BE}•\overrightarrow{CP}=-2×4+0×0+2×4=-8+8=0$,
∴BE⊥CA且BE⊥CP,故BE⊥平面PAC,
(2)由题意可知VF-ABE=VE-ABF,
${S_{△ABF}}=\frac{1}{2}{S_{△PAB}}=\frac{1}{2}×\frac{1}{2}×4\sqrt{2}×4=4\sqrt{2}$
又由$\left\{{\begin{array}{l}{\overrightarrow{AB}=({4,-4,0})}\\{\overrightarrow{AF}=({2,-2,2})}\end{array}}\right.$可求得平面ABF的一个法向量$\overrightarrow n=({1,1,0})$
而$\overrightarrow{AE}=({2,-4,2})$,∴E到平面ABF的距离$d=\left|{\left.{\frac{{\overrightarrow n•\overrightarrow{AE}}}{{\left|{\left.{\overrightarrow n}\right|}\right.}}}\right|}\right.=\left|{\left.{\frac{2-4}{{\sqrt{2}}}}\right|}\right.=\sqrt{2}$
∴${V_{F-ABE}}={V_{E-ABF}}=\frac{1}{3}{S_{△ABF}}•d=\frac{1}{3}×4\sqrt{2}×\sqrt{2}=\frac{8}{3}$.
点评 本题考查直线与平面垂直,几何体的体积的求法,几何法与向量法的应用,考查转化思想以及逻辑推理能力.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点,下列说法正确的是②③④.(填上所有正确命题的序号)
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点,下列说法正确的是②③④.(填上所有正确命题的序号)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知直三棱柱ABC-A′B′C′满足∠BAC=90°,AB=AC=$\frac{1}{2}$AA′=2,点M,N分别为A′B,B′C′的中点.
已知直三棱柱ABC-A′B′C′满足∠BAC=90°,AB=AC=$\frac{1}{2}$AA′=2,点M,N分别为A′B,B′C′的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com