
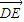 •
•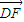 的取值范围;
的取值范围;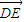 •
•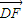 的表达式的取值范围;
的表达式的取值范围;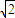 .
.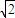 <2
<2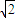 ,所以点N在圆M内,
,所以点N在圆M内,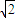 =|2
=|2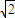 -r|,解得r=
-r|,解得r=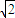 .
.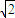 (舍去);
(舍去);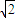 ,0),F(
,0),F(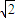 ,0).
,0).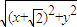 ×
×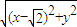 =x2+y2,
=x2+y2,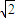 -x,-y),
-x,-y),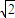 -x,-y),•
-x,-y),•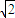 -x)(
-x)(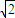 -x)+(-y)(-y)=x2+y2-2=2y2-1,由于点D在圆N内,
-x)+(-y)(-y)=x2+y2-2=2y2-1,由于点D在圆N内,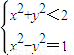 ,由此得y2<
,由此得y2< ,所以
,所以 •
• ∈[-1,0).
∈[-1,0).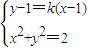 ,
, ,
,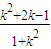 ,
,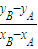 =
=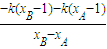 =
= =1=kMN.
=1=kMN.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| DE |
| DF |
查看答案和解析>>
科目:高中数学 来源: 题型:
| PA |
| PB |
查看答案和解析>>
科目:高中数学 来源:2008届第一次六校联考高三数学文科试卷(广州深圳中山珠海惠州) 题型:044
解答时应写出必要的文字说明、证明过程或演算步骤
已知圆M的方程为:(x+3)2+y2=100及定点N(3,0),动点P在圆M上运动,线段PN的垂直平分线交圆M的半径MP于Q点,设点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)试问:过点T(![]() )是否存在直线l,使直线l与曲线C交于A,B两点,且
)是否存在直线l,使直线l与曲线C交于A,B两点,且![]() ,(O为坐标原点)若存在求出直线l的方程,不存在说明理由.
,(O为坐标原点)若存在求出直线l的方程,不存在说明理由.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| PA |
| PB |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省连云港市高一(下)期末数学试卷(A卷)(解析版) 题型:解答题
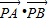 的最小值;
的最小值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com