
【题目】已知f(x)=x2-a|x-1|-1,a∈R.
(1)判断并证明函数f(x)的奇偶性;
(2)若f(x)≥0对x∈[1,+∞)恒成立,求a的取值范围;
(3)写出f(x)在[-2,2]上的最大值g(a).(不需要解答过程)
【答案】(1)答案不唯一,具体见解析(2)(-∞,2](3)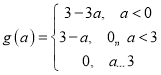
【解析】
(1)验证![]() 即可;
即可;
(2)![]() 对
对![]() 恒成立,则
恒成立,则![]() 对
对![]() 恒成立,分类讨论,即可求
恒成立,分类讨论,即可求![]() 的取值范围;
的取值范围;
(3)分类讨论,去掉绝对值符号,即可写出![]() 在
在![]() ,上的最大值
,上的最大值![]() .
.
解:(1)当a=0时,f(x)=x2-1,f(x)为偶函数,
任意x∈R,f(-x)=(-x)2-1=x2-1=f(x),所以f(x)为偶函数.
当![]() 时
时![]() ,所以非奇非偶.
,所以非奇非偶.
(2)当x∈[1,+∞)时,f(x)=x2-a(x-1)-1=(x-1)(x+1-a).
x=1时,由f(x)≥0成立,得a∈R;
x>1时,由f(x)≥0恒成立,得(x-1)(x+1-a)≥0恒成立,
即x+1-a≥0恒成立,所以a≤x+1对x>1恒成立,
所以a≤2.
综上,a的取值范围是(-∞,2].
(3)f(x)=x2-a|x-1|-1=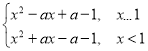
因为函数f(x)=x2-ax+a-1在[1,2]上的最大值=max{f(1),f(2)};
f(x)=x2+ax-a-1在[-2,1]上的最大值=max{f(1),f(-2)}.
所以g(a)=max{f(-2),f(1),f(2)}=max{3-3a,0,3-a}
=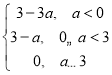


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(-![]() ,0),B(
,0),B(![]() ,0),直线MA,MB交于点M,它们的斜率之积为常数m(m≠0),且△MAB的面积最大值为
,0),直线MA,MB交于点M,它们的斜率之积为常数m(m≠0),且△MAB的面积最大值为![]() ,设动点M的轨迹为曲线E.
,设动点M的轨迹为曲线E.
(1)求曲线E的方程;
(2)过曲线E外一点Q作E的两条切线l1,l2,若它们的斜率之积为-1,那么![]() ·
·![]() 是否为定值?若是,请求出该值;若不是,请说明理由.
是否为定值?若是,请求出该值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (k为常数,e=2.718 28…是自然对数的底数).
(k为常数,e=2.718 28…是自然对数的底数).
(1)当k≤0时,求函数f (x)的单调区间;
(2)若函数f (x)在(0,2)内存在两个极值点,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C:![]() 的离心率为
的离心率为![]() ,右准线方程为
,右准线方程为![]() .
.
![]() 求椭圆C的标准方程;
求椭圆C的标准方程;
![]() 已知斜率存在且不为0的直线l与椭圆C交于A,B两点,且点A在第三象限内
已知斜率存在且不为0的直线l与椭圆C交于A,B两点,且点A在第三象限内![]() 为椭圆C的上顶点,记直线MA,MB的斜率分别为
为椭圆C的上顶点,记直线MA,MB的斜率分别为![]() ,
,![]() .
.
![]() 若直线l经过原点,且
若直线l经过原点,且![]() ,求点A的坐标;
,求点A的坐标;
![]() 若直线l过点
若直线l过点![]() ,试探究
,试探究![]() 是否为定值?若是,请求出定值;若不是,请说明理由.
是否为定值?若是,请求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an} 和等比数列{bn}满足a1=b1=1,a2+a4=10,b2b4=a5.
(1)求{an}的通项公式;
(2)求和:b1+b3+b5+…+b2n-1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一、高二年级的全体学生都参加了体质健康测试,测试成绩满分为100分,规定测试成绩在![]() 之间为“体质优秀”,在
之间为“体质优秀”,在![]() 之间为“体质良好”,在
之间为“体质良好”,在![]() 之间为“体质合格”,在
之间为“体质合格”,在![]() 之间为“体质不合格”
之间为“体质不合格”![]() 现从两个年级中各随机抽取8名学生,测试成绩如下:
现从两个年级中各随机抽取8名学生,测试成绩如下:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
高一年级 | 60 | 85 | 55 | 80 | 65 | 90 | 90 | 75 |
高二年级 | 75 | 85 | 65 | 90 | 75 | 60 | a | b |
其中a,b是正整数.
(1)若该校高一年级有200名学生,试估计高一年级“体质优秀”的学生人数;
(2)从高一年级抽取的学生中再随机选取3人,求这3人中,恰有1人“体质良好”的概率;
(3)设两个年级被抽取学生的测试成绩的平均数相等,当高二年被抽取学生的测试成绩的方差最小时,写出a,b的值![]() 结论不要求证明
结论不要求证明![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司购买了一块长AM=90米,宽AN=30米的矩形地块AMPN,规划建设占地如图中矩形ABCD的仓库,其余地方为道路和停车场,要求顶点C在地块对角线MN上,B、D分别在边AM、AN上,假设AB长度为x米.若规划建设的仓库是高度与AB的长相同的长方体建筑,问AB长为多少时仓库的库容最大?(墙体及楼板所占空间忽略不计)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com