
【题目】已知函数![]() (
(![]() ,e是自然对数的底,
,e是自然对数的底,![]() )
)
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,
,![]() 是函数
是函数![]() 的零点,
的零点,![]() 是
是![]() 的导函数,求证:
的导函数,求证:![]() .
.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增; (2)见解析.
上单调递增; (2)见解析.
【解析】
(1)先求导数,再求导函数零点,再根据![]() 与
与![]() 大小关系分类讨论函数单调性,(2)先研究
大小关系分类讨论函数单调性,(2)先研究![]() 单调性,转化所证不等式为
单调性,转化所证不等式为![]() ,再根据
,再根据![]() 单调性,转化证明
单调性,转化证明![]() 且
且![]() .最后利用不等式性质进行论证.
.最后利用不等式性质进行论证.
(1)![]() ,
,
设![]()
![]() ,
,
解法一:由![]() 和
和![]() 在
在![]() 上单调递增,可知
上单调递增,可知![]() 在
在![]() 上单调递增,
上单调递增,
解法二:由![]() 得
得![]() 可知
可知![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
①当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
②当![]() 时,由
时,由![]() 得
得![]() 或x=1,
或x=1,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
综上所述:当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)解法一(分析法):
当![]() 时,由(1)知
时,由(1)知![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
,
可知![]() ,所以
,所以![]() 在
在![]() 上无零点.
上无零点.
若![]() 是函数
是函数![]() 的零点,则
的零点,则![]() ,
,
∵![]() ,
,
解法一:由![]() 和
和![]() 在
在![]() 上单调递增,且
上单调递增,且![]() 、
、![]() ,可知
,可知![]() 在
在![]() 上单调递增,
上单调递增,
解法二:设![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,
,![]() ,所以
,所以![]() ,
,
可知![]() 在
在![]() 上单调递增,
上单调递增,
要证![]() ,只需证
,只需证![]() ,
,
由(1)知![]() 在
在![]() 上单调递增,
上单调递增,
只需证![]() ,又
,又![]() ,
,
只需证![]() 且
且![]() .
.
![]()
![]() ,
,
由![]() ,
,![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() ;
;
![]() ,由
,由![]() 得
得![]() ,
,
综上所述,得证.
方法二(综合法):
当![]() 时,由(1)知
时,由(1)知![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
,
可知![]() ,所以
,所以![]() 在
在![]() 上无零点.
上无零点.
若![]() 是函数
是函数![]() 的零点,则
的零点,则![]() ,
,
而![]()
![]() ,
,
由![]() ,
,![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() ;
;
![]() ,由
,由![]() 得
得![]() ,
,
所以![]() ,又
,又![]() ,即
,即![]() ,
,
由(1)知![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
而![]() ,
,
由![]() 和
和![]() 在
在![]() 上单调递增,且
上单调递增,且![]() 、
、![]() ,
,
可知![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,得证.
,得证.


科目:高中数学 来源: 题型:
【题目】动点![]() 到直线
到直线![]() 的距离比它到点
的距离比它到点![]() 的距离大1.
的距离大1.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过定点![]() 作直线
作直线![]() ,与(1)中的轨迹
,与(1)中的轨迹![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 为点
为点![]() 关于原点
关于原点![]() 的对称点,证明:
的对称点,证明:![]() ;
;
(3)在(2)中,是否存在垂直于![]() 轴的直线
轴的直线![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在求出
为直径的圆截得的弦长恒为定值?若存在求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京地铁八通线西起四惠站,东至土桥站,全长![]() ,共设13座车站
,共设13座车站![]() 目前八通线执行2014年12月28日制订的计价标准,各站间计程票价
目前八通线执行2014年12月28日制订的计价标准,各站间计程票价![]() 单位:元
单位:元![]() 如下:
如下:
四惠 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
四惠东 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
高碑店 | 3 | span>3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | |||
传媒大学 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
双桥 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
管庄 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
八里桥 | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
通州北苑 | 3 | 3 | 3 | 3 | 3 | ||||||||
果园 | 3 | 3 | 3 | 3 | |||||||||
九棵树 | 3 | 3 | 3 | ||||||||||
梨园 | 3 | 3 | |||||||||||
临河里 | 3 | ||||||||||||
土桥 | |||||||||||||
四惠 | 四惠东 | 高碑店 | 传媒大学 | 双桥 | 管庄 | 八里桥 | 通州北苑 | 果园 | 九棵树 | 梨园 | 临河里 | 土桥 |
![]() 1
1![]() 在13座车站中任选两个不同的车站,求两站间票价为5元的概率;
在13座车站中任选两个不同的车站,求两站间票价为5元的概率;
![]() 2
2![]() 在土桥出站口随机调查了n名下车的乘客,将在八通线各站上车情况统计如下表:
在土桥出站口随机调查了n名下车的乘客,将在八通线各站上车情况统计如下表:
上车站点 | 通州北苑
| 双桥 | 四惠
|
频率 |
| a | b |
人数 | c | 15 | 25 |
求a,b,c,n的值,并计算这n名乘客乘车平均消费金额;
![]() 3
3![]() 某人从四惠站上车乘坐八通线到土桥站,中途任选一站出站一次,之后再从该站乘车
某人从四惠站上车乘坐八通线到土桥站,中途任选一站出站一次,之后再从该站乘车![]() 若想两次乘车花费总金额最少,可以选择中途哪站下车?
若想两次乘车花费总金额最少,可以选择中途哪站下车?![]() 写出一个即可
写出一个即可![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示:在五面体ABCDEF中,四边形EDCF是正方形,AD=DE=1,∠ADE=90°,∠ADC=∠DCB=120°.
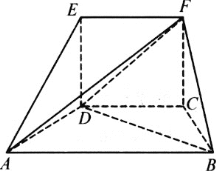
(Ⅰ)求证:平面ABCD⊥平面EDCF;
(Ⅱ)求三棱锥A-BDF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地种植常规稻A和杂交稻B,常规稻A的亩产稳定为500公斤,统计近年来数据得到每年常规稻A的单价比当年杂交稻B的单价高50%.统计杂交稻B的亩产数据,得到亩产的频率分布直方图如下;统计近10年来杂交稻B的单价(单位:元/公斤)与种植亩数(单位:万亩)的关系,得到的10组数据记为![]() ,并得到散点图如下,参考数据见下.
,并得到散点图如下,参考数据见下.
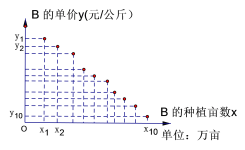
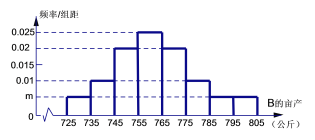
(1)求出频率分布直方图中m的值,若各组的取值按中间值来计算,求杂交稻B的亩产平均值;
(2)判断杂交稻B的单价y(单位:元/公斤)与种植亩数x(单位:万亩)是否线性相关,若相关,试根据以下统计的参考数据求出y关于x的线性回归方程;
(3)调查得到明年此地杂交稻B的种植亩数预计为2万亩,估计明年常规稻A的单价,若在常规稻A和杂交稻B中选择,明年种植哪种水稻收入更高?
统计参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
附:线性回归方程![]() ,
,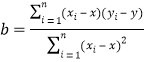 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
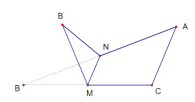
【题目】如图,∠C=![]() ,
,![]() ,M,N分别是BC,AB的中点,将△BMN沿直线MN折起,使二面角B'-MN-B的大小为
,M,N分别是BC,AB的中点,将△BMN沿直线MN折起,使二面角B'-MN-B的大小为![]() ,则B'N与平面ABC所成角的正切值是( )
,则B'N与平面ABC所成角的正切值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点F,直线y=4与y轴的交点为P,与抛物线C的交点为Q,且|QF|=2|PQ|.
(1)求p的值;
(2)已知点T(t,-2)为C上一点,M,N是C上异于点T的两点,且满足直线TM和直线TN的斜率之和为![]() ,证明直线MN恒过定点,并求出定点的坐标.
,证明直线MN恒过定点,并求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 给出求羡除体积的“术”是:“并三广,以深乘之,又以袤乘之,六而一”,其中的“广”指羡除的三条平行侧棱的长,“深”指一条侧棱到另两条侧棱所在平面的距离,“袤”指这两条侧棱所在平行线之间的距离,用现代语言描述:在羡除
给出求羡除体积的“术”是:“并三广,以深乘之,又以袤乘之,六而一”,其中的“广”指羡除的三条平行侧棱的长,“深”指一条侧棱到另两条侧棱所在平面的距离,“袤”指这两条侧棱所在平行线之间的距离,用现代语言描述:在羡除![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,两条平行线
,两条平行线![]() 与
与![]() 间的距离为h,直线
间的距离为h,直线![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则该羡除的体积为
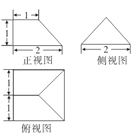
,则该羡除的体积为![]() 已知某羡除的三视图如图所示,则该羡除的体积为
已知某羡除的三视图如图所示,则该羡除的体积为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com