
(08年岳阳一中二模文)(13分) 如图,在底面是菱形的四棱锥P―ABCD中,∠ABC=600,PA=AC=a,PB=PD=![]() ,点E
,点E
在PD上,且PE:ED=2:1。
(1)证明PA⊥平面ABCD;
(2)求以AC为棱,EAC与DAC为面的二面角![]() 的大小;
的大小;
(3)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论。

解析:证明: (Ⅰ) 因为底面ABCD是菱形,∠ABC=60°,
所以AB=AD=AC=a, 在△PAB中,
由PA2+AB2=2a2=PB2 知PA⊥AB.
同理,PA⊥AD,所以PA⊥平面ABCD…………3分
(Ⅱ)解 作EG//PA交AD于G,
由PA⊥平面ABCD.
知EG⊥平面ABCD.作GH⊥AC于H,连结EH,则EH⊥AC,∠EHG即为二面角![]() 的平面角.
的平面角.
又PE : ED=2 : 1,所以![]()
从而 ![]()
![]() ……………7分
……………7分
 (Ⅲ)解法一 以A为坐标原点,直线AD、AP分别为y轴、z轴,过A点垂直平面PAD的直线为x轴,建立空间直角坐标系如图.由题设条件,相关各点的坐标分别为
(Ⅲ)解法一 以A为坐标原点,直线AD、AP分别为y轴、z轴,过A点垂直平面PAD的直线为x轴,建立空间直角坐标系如图.由题设条件,相关各点的坐标分别为
![]()
![]()
所以 ![]()
![]()
![]()
设点F是棱PC上的点,![]() 则
则
![]()
![]() 令
令 ![]() 得
得
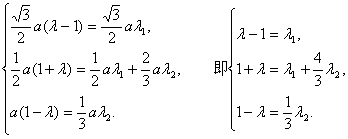
解得 ![]() 即
即 ![]() 时,
时,![]()
亦即,F是PC的中点时,![]() 、
、![]() 、
、![]() 共面.
共面.
又 BF![]() 平面AEC,所以当F是棱PC的中点时,BF//平面AEC
平面AEC,所以当F是棱PC的中点时,BF//平面AEC
|
解法二 当F是棱PC的中点时,BF//平面AEC,证明如下,
证法一 取PE的中点M,连结FM,则FM//CE. ①
由 ![]() 知E是MD的中点.
知E是MD的中点.
连结BM、BD,设BD![]() AC=O,则O为BD的中点.
AC=O,则O为BD的中点.
所以 BM//OE. ②
由①、②知,平面BFM//平面AEC.
又 BF![]() 平面BFM,所以BF//平面AEC.
平面BFM,所以BF//平面AEC.
证法二因为 ![]()

所以 ![]() 、
、![]() 、
、![]() 共面.
共面.
又 BF![]() 平面ABC,从而BF//平面AEC.
平面ABC,从而BF//平面AEC.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:高中数学 来源: 题型:
(08年岳阳一中二模理)(12分) 一个盒子中装有6张卡片,上面分别写着如下6个定义域均为R的函数:
![]() .
.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得到一个新函数,求所得函数
为奇函数的概率;
(2)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行。求抽取次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年岳阳一中二模理)(12分) 已知梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
, ![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ∥
∥![]() ,
,![]() ,
,![]() 是
是![]() 的中点,沿
的中点,沿![]() 将 梯形
将 梯形![]() 翻折,使平面
翻折,使平面![]() 平面
平面![]() (如图)。
(如图)。
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)若以F、B、C、D为顶点的三棱锥的体积记为![]() ,求
,求![]() 的最大值;当
的最大值;当![]() 取得最大值时,求二面角D-BF-C的大小。
取得最大值时,求二面角D-BF-C的大小。


查看答案和解析>>
科目:高中数学 来源: 题型:
(08年岳阳一中二模理)(13分) 对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点。如果函数
的不动点。如果函数![]() 有且仅有两个不动点
有且仅有两个不动点![]() 、
、![]() ,且
,且![]() 。
。
(1)试求函数![]() 的单调区间;
的单调区间;
(2)已知各项不为零的数列![]() 满足
满足![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年岳阳一中二模文)(12分)
有A、B、C、D、E五支足球队参加某足球邀请赛,比赛采用单循环制,每场比赛胜队得3分,负队得0分;若为平局则双方各得1分。已知任何一个队打胜、打平或被打败的概率都是![]() 。
。
(1) 求打完全部比赛A队取得3分的概率;
(2) 求打完全部比赛A队胜的次数多于负的次数的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年岳阳一中二模文)(12分)
设数列![]() 的各项都是正数,且对任意
的各项都是正数,且对任意![]() ,都有
,都有![]() ,记
,记![]() 为数列
为数列![]() 的前
的前![]() 项和。
项和。
(1) 求证:![]() ;
;
(2) 求数列![]() 的通项公式;
的通项公式;
(3) 若![]() (
(![]() 为非零常数,
为非零常数,![]() ),问是否存在整数
),问是否存在整数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com