
【题目】如图所示,某街道居委会拟在![]() 地段的居民楼正南方向的空白地段
地段的居民楼正南方向的空白地段![]() 上建一个活动中心,其中
上建一个活动中心,其中![]() 米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形
米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形![]() ,上部分是以
,上部分是以![]() 为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长
为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长![]() 不超过
不超过![]() 米,其中该太阳光线与水平线的夹角
米,其中该太阳光线与水平线的夹角![]() 满足
满足![]() .
.

(1)若设计![]() 米,
米,![]() 米,问能否保证上述采光要求?
米,问能否保证上述采光要求?
(2)在保证上述采光要求的前提下,如何设计![]() 与
与![]() 的长度,可使得活动中心的截面面积最大?(注:计算中
的长度,可使得活动中心的截面面积最大?(注:计算中![]() 取3)
取3)
【答案】(Ⅰ)能(Ⅱ)![]() 米且
米且![]() 米
米
 【解析】
【解析】
试题分析:(Ⅰ)由条件知研究直线与圆相切,所以建立坐标系:以点A为坐标原点,AB所在直线为x轴,,确定圆的方程,求出切线方程![]() ,解出切线与直线交点,最后判断
,解出切线与直线交点,最后判断![]() 是否满足不超过
是否满足不超过![]() 米这个条件(Ⅱ)同(1)建立坐标系,设立圆的方程:圆心为
米这个条件(Ⅱ)同(1)建立坐标系,设立圆的方程:圆心为![]() ,半径为
,半径为![]() ,求出切线方程
,求出切线方程![]() ,解出切线与直线交点,根据
,解出切线与直线交点,根据 ![]() 不超过
不超过![]() 米这个条件列参数限制条件
米这个条件列参数限制条件![]() ,最后根据活动中心的截面面积关系式求最值:
,最后根据活动中心的截面面积关系式求最值:![]()
![]()
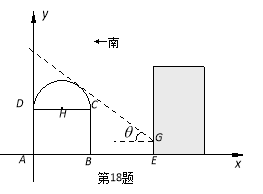
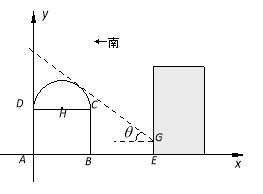
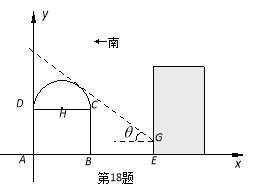
试题解析:解:如图所示,以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系.
(1)因为![]() ,
,![]() ,所以半圆的圆心为
,所以半圆的圆心为![]() ,
,
半径![]() .设太阳光线所在直线方程为
.设太阳光线所在直线方程为![]() ,
,
即![]() , ...............2分
, ...............2分
则由![]() ,
,
 解得
解得![]() 或
或![]() (舍).
(舍).
故太阳光线所在直线方程为![]() , ...............5分
, ...............5分
令![]() ,得
,得![]() 米
米![]() 米.
米.
所以此时能保证上述采光要求. ...............7分
(2)设![]() 米,
米,![]() 米,则半圆的圆心为
米,则半圆的圆心为![]() ,半径为
,半径为![]() .
.
方法一:设太阳光线所在直线方程为![]() ,
,
即![]() ,由
,由![]() ,
,
解得![]() 或
或![]() (舍). ...............9分
(舍). ...............9分
故太阳光线所在直线方程为![]() ,
,
令![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() . ...............11分
. ...............11分
所以![]()
![]() .
.
当且仅当![]() 时取等号.
时取等号.
所以当![]() 米且
米且![]() 米时,可使得活动中心的截面面积最大. .............16分
米时,可使得活动中心的截面面积最大. .............16分
方法二:欲使活动中心内部空间尽可能大,则影长EG恰为![]() 米,则此时点
米,则此时点![]() 为
为![]() ,
,
设过点G的上述太阳光线为![]() ,则
,则![]() 所在直线方程为y-=-(x-30),
所在直线方程为y-=-(x-30),
即![]() . ........10分
. ........10分
由直线![]() 与半圆H相切,得
与半圆H相切,得![]() .
.
而点H(r,h)在直线![]() 的下方,则3r+4h-100<0,
的下方,则3r+4h-100<0,
即![]() ,从而
,从而![]() . ...............13分
. ...............13分
又![]()
![]() .
.
当且仅当![]() 时取等号.
时取等号.
所以当![]() 米且
米且![]() 米时,可使得活动中心的截面面积最大. ...........16分
米时,可使得活动中心的截面面积最大. ...........16分


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】在上海自贸区的利好刺激下,![]() 公司开拓国际市场,基本形成了市场规模;自2014年1月以来的第
公司开拓国际市场,基本形成了市场规模;自2014年1月以来的第![]() 个月(2014年1月为第一个月)产品的内销量、出口量和销售总量(销售总量=内销量+出口量)分别为
个月(2014年1月为第一个月)产品的内销量、出口量和销售总量(销售总量=内销量+出口量)分别为![]() 、
、![]() 和
和![]() (单位:万件),依据销售统计数据发现形成如下营销趋势:
(单位:万件),依据销售统计数据发现形成如下营销趋势:![]() ,
,![]() (其中
(其中![]() ,
,![]() 为常数,
为常数,![]() ),已知
),已知![]() 万件,
万件,![]() 万件,
万件,![]() 万件.
万件.
(1)求![]() ,
,![]() 的值,并写出
的值,并写出![]() 与
与![]() 满足的关系式;
满足的关系式;
(2)证明:![]() 逐月递增且控制在2万件内;
逐月递增且控制在2万件内;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点.
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ![]() ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为- ![]() .
. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个路灯的平面设计示意图,其中曲线段AOB可视为抛物线的一部分,坐标原点O为抛物线的顶点,抛物线的对称轴为y轴,灯杆BC可视为线段,其所在直线与曲线AOB所在的抛物线相切于点B.已知AB=2分米,直线![]() 轴,点C到直线AB的距离为8分米.灯杆BC部分的造价为10元/分米;若顶点O到直线AB的距离为t分米,则曲线段AOB部分的造价为
轴,点C到直线AB的距离为8分米.灯杆BC部分的造价为10元/分米;若顶点O到直线AB的距离为t分米,则曲线段AOB部分的造价为![]() 元. 设直线BC的倾斜角为,以上两部分的总造价为S元.
元. 设直线BC的倾斜角为,以上两部分的总造价为S元.
(1)①求t关于的函数关系式;
②求S关于的函数关系式;
(2)求总造价S的最小值.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别是长轴长为 ![]() 的椭圆C:
的椭圆C: ![]() 的左右焦点,A1 , A2是椭圆C的左右顶点,P为椭圆上异于A1 , A2的一个动点,O为坐标原点,点M为线段PA2的中点,且直线PA2与OM的斜率之积恒为﹣
的左右焦点,A1 , A2是椭圆C的左右顶点,P为椭圆上异于A1 , A2的一个动点,O为坐标原点,点M为线段PA2的中点,且直线PA2与OM的斜率之积恒为﹣ ![]() .
.
(1)求椭圆C的方程;
(2)设过点F1且不与坐标轴垂直的直线C(2,2,0)交椭圆于A,B两点,线段AB的垂直平分线与B(2,0,0)轴交于点N,点N横坐标的取值范围是 ![]() ,求线段AB长的取值范围.
,求线段AB长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项的和.
项的和.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() ,18,
,18,![]() 成等比数列,求正整数
成等比数列,求正整数![]() 的值;
的值;
(3)是否存在![]() ,使得
,使得![]() 为数列
为数列![]() 中的项?若存在,求出所有满足条件的
中的项?若存在,求出所有满足条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心![]() 为的圆,满足下列条件:圆心
为的圆,满足下列条件:圆心![]() 位于
位于![]() 轴正半轴上,与直线
轴正半轴上,与直线![]() 相切且被轴
相切且被轴![]() 截得的弦长为
截得的弦长为![]() ,圆
,圆![]() 的面积小于13.
的面积小于13.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() .是否存在这样的直线
.是否存在这样的直线![]() ,使得直线
,使得直线![]() 与
与![]() 恰好平行?如果存在,求出
恰好平行?如果存在,求出![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com