
 恒成立;③要满足y的最大值小于8.
恒成立;③要满足y的最大值小于8.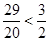 ,即y≥
,即y≥ 不恒成立,不满足条件②,故该函数模型不符合该单位报销方案.(6分)
不恒成立,不满足条件②,故该函数模型不符合该单位报销方案.(6分) =
= ≥0.∴f(x)在[2,10]上是增函数,满足条件①.由条件②,得x-2lnx+a≥
≥0.∴f(x)在[2,10]上是增函数,满足条件①.由条件②,得x-2lnx+a≥ ,即a≥2lnx-
,即a≥2lnx- 在x∈[2,10]上恒成立,令g(x)=2lnx-
在x∈[2,10]上恒成立,令g(x)=2lnx- ,则g′(x)=
,则g′(x)= -
- =
= ,由g′(x)>0得0<x<4,∴g(x)在(0,4)上是增函数,在(4,10)上是减函数.
,由g′(x)>0得0<x<4,∴g(x)在(0,4)上是增函数,在(4,10)上是减函数.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 (单位:元)与上市时间
(单位:元)与上市时间 (单位:天)的数据如下:
(单位:天)的数据如下:上市时间 天 天 | 4 | 10 | 36 |
市场价 元 元 | 90 | 51 | 90 |
 与上市时间
与上市时间 的变化关系并说明理由:①
的变化关系并说明理由:①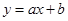 ;②
;② ;③
;③ .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
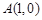 ,点
,点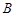 在曲线
在曲线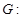
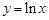 上,若线段
上,若线段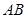 与曲线
与曲线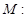
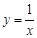 相交且交点恰为线段
相交且交点恰为线段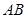 的中点,则称
的中点,则称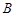 为曲线
为曲线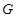 关于曲线
关于曲线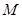 的一个关联点.那么曲线
的一个关联点.那么曲线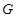 关于曲线
关于曲线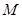 的关联点的个数为( )
的关联点的个数为( )| A.0 | B.1 | C.2 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 上的函数
上的函数 满足:对于任意的
满足:对于任意的 ,都有
,都有 ,且
,且 时,有
时,有 ,
, 的最大值、最小值分别为
的最大值、最小值分别为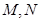 ,则
,则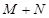 的值为( )
的值为( )| A.2012 | B.2013 | C.4024 | D.4026 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,x∈A,y∈B,满足条件的对应法则f构成从集合A到集合B的函数;
,x∈A,y∈B,满足条件的对应法则f构成从集合A到集合B的函数;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com