
分析 (1)因为直线l1的倾斜角为30°,所以$\frac{b}{a}=\frac{\sqrt{3}}{3}$,因为双曲线的焦距为4$\sqrt{2}$,所以c=4再根据a,b,c关系,可得椭圆方程.
(2)设直线l的方程为:my=x-2.与椭圆的方程联立可得根与系数的关系,利用弦长公式可得弦弦长|AB|,利用点到直线的距离公式可得原点到直线l的距离d,再利用S△OAB=$\frac{1}{2}$|AB|d,导利用基本不等式求最值,及直线方程,再求圆的弦.
解答 解:(1)由已知得$\frac{b}{a}=\frac{\sqrt{3}}{3}$,a2+b2=8.解得:a2=6,b2=2,∴椭圆C的方程为:$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$.
(2)解:∵椭圆C的右焦点F(2,0),故设直线l的方程为:x=my+2.
联立$\left\{\begin{array}{l}{x=my+2}\\{{x}^{2}+3{y}^{2}=6}\end{array}\right.$得化为(3+m2)y2+4my-2=0.
|AB|=$\sqrt{1+{m}^{2}}\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{2\sqrt{6}({m}^{2}+1)}{3+{m}^{2}}$,点O到直线l的距离d=$\frac{2}{\sqrt{1+{m}^{2}}}$.
S△OAB=$\frac{1}{2}$|AB|d=$\frac{2\sqrt{6}\sqrt{{m}^{2}+1}}{3+{m}^{2}}$,
令$\sqrt{{m}^{2}+1}$=t≥1,S△OAB=f(t)=$\frac{2\sqrt{6}t}{{t}^{2}+2}=\frac{2\sqrt{6}}{t+\frac{2}{t}}≤\sqrt{3}$,
当t=$\sqrt{2}$,即m=±1时,△OAB的面积最大.
此时直线l的方程为:x=±y+2,
圆心O到直线l的距离为d1=$\sqrt{2}$,DE=2$\sqrt{{r}^{2}-{{d}_{1}}^{2}}=4$.
点评 本题考查了直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式、利用基本不等式求最值,考查了推理能力与计算能力,属于难题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
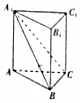 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1B1BA,且AA1=AB=BC=2,则AC与平面A1BC所成角为( )
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1B1BA,且AA1=AB=BC=2,则AC与平面A1BC所成角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com