
【题目】在直角坐标系xOy中,直线l的参数方程为  (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2 ![]() sinθ.
sinθ.
(1)求圆C的直角做标方程;
(2)圆C的圆心为C,点P为直线l上的动点,求|PC|的最小值.
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足 ![]()
![]() =0,
=0, ![]() =2
=2 ![]() .
.
(1)当点P在圆上运动时,求点Q的轨迹方程;
(2)若斜率为k的直线 l与圆x2+y2=1相切,直线 l与(1)中所求点Q的轨迹交于不同的两点F,H,O是坐标原点,且 ![]() ≤
≤ ![]()
![]() ≤
≤ ![]() 时,求k的取值范围.
时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某跳水运动员在一次跳水训练时的跳水曲线为如图所示抛物线的一段.已知跳水板![]() 长为
长为![]() ,跳水板距水面
,跳水板距水面![]() 的高
的高![]() 为
为![]() .为安全和空中姿态优美,训练时跳水曲线应在离起跳点
.为安全和空中姿态优美,训练时跳水曲线应在离起跳点![]() 处水平距
处水平距![]()
![]() 时达到距水面最大高度
时达到距水面最大高度![]() ,规定:以
,规定:以![]() 为横轴,
为横轴,![]() 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.
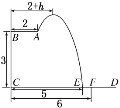
(1)当![]() 时,求跳水曲线所在的抛物线方程;
时,求跳水曲线所在的抛物线方程;
(2)若跳水运动员在区域![]() 内入水时才能达到比较好的训练效果,求此时
内入水时才能达到比较好的训练效果,求此时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E,F分别是棱A1B1 , B1C1的中点,O是AC与BD的交点,面OEF与面BCC1B1相交于m,面OD1E与面BCC1B1相交于n,则直线m,n的夹角为( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an= ![]() ,若从{an}中提取一个公比为q的等比数列{
,若从{an}中提取一个公比为q的等比数列{ ![]() },其中k1=1,且k1<k2<…<kn , kn∈N* , 则满足条件的最小q的值为 .
},其中k1=1,且k1<k2<…<kn , kn∈N* , 则满足条件的最小q的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sin(x+ ![]() )的图象上各点的横坐标压缩为原来的
)的图象上各点的横坐标压缩为原来的 ![]() 倍(纵坐标不变),所得函数在下面哪个区间单调递增( )
倍(纵坐标不变),所得函数在下面哪个区间单调递增( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的增函数,函数y=f(x﹣1)的图象关于点(1,0)对称,若对任意的x,y∈R,等式f(y﹣3)+f( ![]() )=0恒成立,则
)=0恒成立,则 ![]() 的取值范围是( )
的取值范围是( )
A.[2﹣ ![]()
![]() ,2+
,2+ ![]()
![]() ]
]
B.[1,2+ ![]()
![]() ]
]
C.[2﹣ ![]()
![]() ,3]
,3]
D.[1,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com