
���� ���ܱ�3����1�ұ�5����1���������ܱ�15������1���������õȲ�����ͨ�ʽ���Լ��ⲻ��ʽ���ɵõ�����������
��� �⣺���ܱ�3����1�ұ�5����1���������ܱ�15������1������
��an=15n-14��
��an=15n-14��2016
��n��135���ʴ����е�����Ϊ135��
�ʴ�Ϊ��135��
���� ���⿼������ģ����ʵ�������е�Ӧ�ã�����Ȳ����е�ͨ�ʽ�����ã������������������ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
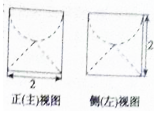 ��ijԲ������ϲ��ڵ�һ�������²��ڵ�һ��Բ�����õļ����������ͼ�е�����������ͼ�Ͳࣨ����ͼ��ͼ��ʾ����˼�����ı�����ǣ�������
��ijԲ������ϲ��ڵ�һ�������²��ڵ�һ��Բ�����õļ����������ͼ�е�����������ͼ�Ͳࣨ����ͼ��ͼ��ʾ����˼�����ı�����ǣ�������| A�� | ��4+$\sqrt{2}$���� | B�� | 6$��+2\sqrt{2}��$ | C�� | 6$��+\sqrt{2}��$ | D�� | ��8+$\sqrt{2}$���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{33}{15}$ | B�� | $\frac{33}{15}$ | C�� | -$\frac{33}{17}$ | D�� | $\frac{33}{17}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {3��5} | B�� | {1��3��4��5��6��7��8} | C�� | {2��8} | D�� | {1��7} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com